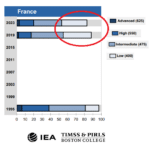
Paradoxe : second pays du monde pour les médailles Fields, la France est dans les derniers pays développés quand il s’agit d’évaluer le niveau en maths de ses élèves. Pour expliquer et dépasser ce paradoxe, dans « Réussir en maths à l’école, c’est possible (Hatier), Roland Charnay invite à réfléchir aux remèdes à apporter à l’enseignement des maths. En s’appuyant sur sa longue expérience, il écarte les tentations faciles : copier ce qui se fait ailleurs, avoir une confiance aveugle dans une méthode ou une science. Il leur préfère des horizons moins clinquants mais plus surs : former les enseignants, faire confiance à leur professionnalité, veiller aux acquisitions fondamentales. Une réflexion nécessaire au moment où les maths sont devenues un élément de communication politique.
Pourquoi ce livre en ce moment précisément ?
Du fait des débats actuels sur l’enseignement des maths. J’ai souhaité faire entendre une autre proposition car le débat actuel me semble orienté et il est toujours bon de faire entendre des voix différentes.
Dans votre ouvrage vous dites que nos mauvais résultats en maths ne sont pas dus aux programmes. Mais alors à quoi ?
Je dis qu’il y a plusieurs facteurs. Les programmes peuvent être un de ces facteurs. Mais j’observe que dans les pays qui réussissent mieux que nous il ya une différence qui tient d’abord à la politique éducative. Ce sont des pays qui mettent l’accent sur l’éducation, qui donnent des moyens , notamment en formation des enseignants et qui ont une politique éducative continue. En France c’est moins les programmes que leur changement permanent qui pose problème. Depuis 30 ans on a changé de programme de maths au primaire en moyenne une fois tous les 5 ans. C’est justement le temps nécessaire aux enseignants pour assimiler un programme. J’en déduis qu’aucun programme n’a jamais été réellement testé !
En ce moment c’est Singapour qui a le vent en poupe. Vous dites que sa réussite n’est pas liée à une méthode. Pourquoi ?
De nombreux facteurs peuvent expliquer l’excellente place de Singapour dans les classements mondiaux. La varie méthode de Singapour c’est une politique éducative . Quand on parle de « méthode de Singapour » parle-t-on de la politique de l’Etat, de l’approche des maths ou de l’adaptation d’un ouvrage proposé en France ?
Le point fondamental à Singapour c’est la formation des enseignants. Or en France elle a été abandonnée pendant plusieurs années. Le rapport Villani insiste lui aussi sur ce point mais sera-t-il écouté ?
Vous dites aussi que manipuler ne suffit pas pour apprendre les maths. Que voulez vous dire ?
Tout le monde est d’accord avec l’idée que les enfants doivent apprendre les maths à partir du réel. Mais jouer avec des objets ça n’a jamais provoqué l’apprentissage des maths. Ce qui fait apprentissage c’est quand une manipulation est orientée par un questionnement, une problématique. Ce sont les problèmes posés qui débouchent sur l’apprentissage. Là on touche une faiblesse de Singapour en ce qui concerne la résolution de problèmes.
Mais vous écrivez que la résolution de problèmes ne suffit pas non plus…
Elle est à la base de certains concepts mathématiques. Mais pour que les concepts soient appropriés il faut un travail de structuration par les enseignants. Il faut de la révision, un entrainement, de la familiarisation. Comme dit G Vergnaud c’est un point de départ. C’ets la question qui donne du sens au concept. Une fois celui ci élaboré il doit pouvoir être utilisé dans d’autres contextes.
Si l’on veut que le niveau en mathématiques s’améliore, que doit on faire ?
Je propose des pistes à la fin du livre. Il faut déjà se défier des tentations nostalgiques comme revenir à un âge d’or , qui n’a jamais existé, où il n’y avait pas de machine à calculer. Il faut aussi résister à la tentation de l’ailleurs : penser que transposer directement une expérience étrangère serait la solution. Si on regarde de près Singapour par exemple, on voit que le système éducatif est très coercitif, qu’il y a beaucoup de cours particuliers. On ne peut pas simplement transposer car il y a des différences sociales et culturelles énormes.
Enfin il faut résister à la tentation scientiste. Les neurosciences apportent des choses intéressantes mais l’apprentissage des maths ne peut pas se réduire à ce seul apport. Pour penser cet enseignement il faut aussi regarder du coté de l’enfant, de la psychologie cognitive et aussi voir le coté de l’élève en classe avec d’autres élèves et un prof et des phénomènes didactiques.
Ma principale orientation dans ce livre c’est la formation des enseignants. IL faudrait aussi recruter autrement c’est à dire des enseignants du premier degré ayant plus de formation mathématique. Il faudrait leur faire confiance. Par exemple que l’évaluation ne soit pas un moyen de coercition mais un outil mis à leur disposition.
J’ouvre aussi une autre piste : faire que les savoirs enseignés soient davantage hiérarchisés. Il faudrait enseigner moins de choses mais de façon plus approfondie. Et organiser cet enseignement autour de fondamentaux comme la numération décimale ou le calcul mental. Il faut que les enfants acquièrent le sens des opérations , c’est à dire qu’ils assimilent qu’une même opération peut résoudre des catégories de problèmes différentes et qu’il y a un lien entre les opérations.
Enfin il faut aussi privilégier la résolution de problèmes. Dans PIsa on voit bien que les jeunes français ont des connaissances mais manquent de capacité à les utiliser dans des situations moins scolaires. I faut donc apprendre aux élèves des stratégies de recherche.
Propos recueillis par François Jarraud
Roland Charnay, Réussir en maths à l’école c’est possible ! , Hatier, 2018, ISBN 978-2-401-03326-9
