Le ministère vient de publier des repères annuels de progression pour les classes de l’école élémentaire. Dès le cycle 2, la progressivité adoptée est l’exact contraire de celle qui prévalait dans le programme 2015. Il existe en effet deux grands types de progression à ce niveau de la scolarité : soit les élèves apprennent d’emblée l’écriture des grands nombres en s’appuyant sur les régularités verbales et une file numérotée : quand j’entends « vingt » l’écriture commence par le chiffre « 2 », soit ils découvrent plus tardivement cette écriture mais de façon conceptuelle : quand j’entends « vingt », le nombre contient 2 dizaines et, donc, l’écriture commence par le chiffre « 2 ».
Le premier choix a prévalu entre 1986 et 2015 et il s’est accompagné d’un effondrement des performances en calcul des écoliers français. L’une des nouveautés majeures du programme 2015 était de renouer avec une approche progressive et conceptuelle de l’écriture des nombres. Il est important que les professeurs puissent continuer de le faire. Le choix pédagogique de progresser plus lentement mais de s’appuyer d’emblée sur la compréhension chez les élèves, ne peut pas être ôté aux professeurs des écoles.
Au CP, des progressivités complètement différentes en 2015 et 2018
 Comparons les repères de progressivité qui figurent dans le programme de CP en 2015 et en 2018 respectivement :
Comparons les repères de progressivité qui figurent dans le programme de CP en 2015 et en 2018 respectivement :
• En 2015, on lisait : « Au CP, l’étude systématique des relations numériques entre des nombres inférieurs à 10, puis à 20 (décomposition/recomposition), est approfondie durant toute l’année. Parallèlement, l’étude de la numération décimale écrite en chiffres (dizaines, unités simples) pour les nombres jusqu’à 100 et celle de la désignation orale, permet aux élèves de dénombrer et constituer des collections de plus en plus importantes […]. »
• En 2018, on lit : « Dès le début de l’année, les élèves étudient de façon systématique la numération décimale écrite en chiffres (dizaines, unités simples) pour les nombres jusqu’à 100. La désignation orale des nombres est démarrée en période 3 : « 53, c’est 5 dizaines et 3 unités ; c’est (5 fois 10) et (3 fois 1) ».
L’étude des 10 premiers nombres doit être progressive
Les repères 2015 constituaient une mise en garde : attention, l’étude des nombres au CP doit se faire progressivement, d’abord jusqu’à 10 puis jusqu’à 20, il faut se garder de vouloir aller trop vite. De nombreux élèves de CP, en décembre, ne se sont pas encore approprié la propriété conceptuelle qui fonde le nombre : la propriété « +1 répété », qu’on appelle aussi l’itération de l’unité. Si, face à un tas de jetons, on leur demande d’en donner 8, ils savent évidemment le faire en comptant-numérotant 12345678, 8. Mais si, à la suite, l’enseignant déclare en vouloir 9, de nombreux élèves sont incapables d’ajouter 1 nouveau jeton à la collection de 8 déjà formée ; ils sont obligés de recompter 123456789, 9.
C’est la raison pour laquelle Henri Canac, l’un des grands pédagogues de la période ayant suivi la libération de la France, préconisait d’aborder les premiers nombres l’un après l’autre, dans l’ordre, en conduisant les élèves à : « construire (définir, poser), le nouveau nombre par adjonction de l’unité au nombre précédent, puis à étudier ses diverses décompositions en nombres moins élevés que lui. »
Il ne faut pas considérer cette progressivité comme la lubie d’un pédagogue isolé dans son coin parce que Henri Canac précise qu’elle est le fruit de décennies de réflexion de la profession. Il écrit en 1947 que cette « méthode nouvelle …/… forme à (son) sens, une des meilleures conquêtes de la pratique pédagogique au cours du dernier quart de siècle. » En fait, quiconque s’intéresse à l’histoire des pratiques et des discours pédagogiques sait qu’un tournant dans ceux-ci commence avec la publication des programmes officiels de 1923 et celle des textes pédagogiques qui les entourent. C’est à cette époque que la « méthode nouvelle » qu’évoque Henri Canac commence à s’élaborer.
L’effet délétère du basculement de 1986
Or, cette méthode nouvelle est abandonnée après 1986, date d’une circulaire pour l’école maternelle publiée alors que Jean-Pierre Chevènement est ministre de l’éducation nationale. On lit dans cette circulaire que : « (l’enfant) apprend et récite la comptine numérique » alors qu’en 1982 encore, il était écrit dans une revue qui faisait référence à l’époque, Le Monde de l’éducation, que « Pour des enfants de cinq ans, apprendre à compter jusqu’à 10 n’a guère d’utilité (sinon faire plaisir aux parents) ». Sans le savoir, le ministre de l’époque a importé en France la culture pédagogique états-unienne des premiers apprentissages numériques (voir Brissiaud 2013).
Il est encore plus intéressant de noter qu’une étude de la Direction de l’évaluation, de la prospective et de la performance (DEPP) datant de 2008 montre que les performances en calcul des écoliers français se sont effondrées entre 1987 et 1999, c’est-à-dire immédiatement après que le ministère ait demandé aux professeurs des écoles d’enseigner les nombres à rebours de toutes les recommandations antérieures. Pour donner une idée de l’ampleur de cet effondrement et de son contexte pédagogique, il faut noter que la baisse des performances correspond à une année d’apprentissage du calcul en moins si l’on se réfère à des enquêtes sociologiques analogues.
Or les écoliers de 1987, ceux qui calculaient encore bien, étudiaient principalement à partir d’une méthode qui s’appelait « Maths et calcul » (l’auteur était Eiler) ou d’une autre dont l’auteur était Thevenet et qui s’inspirait beaucoup de la première. Dans ces méthodes, la première leçon sur les nombres, celle sur les nombres 1, 2 et 3 s’effectuait en décembre au CP. Dans l’ouvrage pédagogique « savant » qui servait de référence à l’époque, Ermel 1977, l’écriture des premiers nombres ne commençait pas avant janvier au CP. Ces élèves qui avaient commencé tardivement leur apprentissage scolaire de l’écriture des nombres, se révélaient avoir environ 1 an d’avance au CM2 par rapport à ceux d’aujourd’hui ! Dans un rapport d’inspecteurs généraux qui accompagnait les programmes officiels de 1923, on pouvait lire : « il y a des retards apparents qui valent bien des avances ».
L’effet délétère d’un apprentissage behavioriste de l’écriture des numéros après 10
Les professeurs qui s’inspireront des repères de progressivité 2018 enseigneront l’écriture des 100 premiers numéros dès le début du CP. Les enfants apprendront à mémoriser les écritures chiffrées après 9 comme ils l’on fait des premiers chiffres : pour accéder à l’écriture de « treize », par exemple, il suffit en effet de compter-numéroter les premières cases d’une file numérotée jusqu’à entendre « treize » : l’élève compte les cases de la file 1,2,3,4,5,6,7,8,9,10,11,12,13. À ce moment, il entend « treize » et il s’arrête. Dans la case sur laquelle il s’est arrêté, il voit écrit un « 1 » et un « 3 » juxtaposés, il est ainsi capable de produire l’écriture de « treize » : c’est 13.
C’est plus tard seulement que les élèves seront initiés au fait que le « 1 » de l’écriture de « treize » s’explique par la décomposition 10+3, c’est-à-dire que l’écriture des nombres après 10 s’explique par un dénombrement des collections où l’on commence par former 1 dizaine. Ainsi, avec les repères de progressivité 2018, l’apprentissage est d’abord de type associatif (on dit aussi « behavioriste »), la compréhension, elle, étant différée de plusieurs mois. Rappelons qu’on lit dans le document que « La désignation orale des nombres est démarrée en période 3 : « 53, c’est 5 dizaines et 3 unités ; c’est (5 fois 10) et (3 fois 1) »
Or, au moment où l’on dira aux élèves que 11=10+1, 12=10+2, 13=10+3, etc. ils n’auront plus besoin de ces décompositions pour lire et écrire ces nombres parce que, par la répétition, ils auront associé le nom du numéro et son écriture. L’enseignant fera des leçons de numération mais elles fonctionneront très mal avec les élèves les plus fragiles qui ne comprendront pas pourquoi on les embête avec les décompositions précédentes alors qu’ils savent déjà lire et écrire ces nombres ou, du moins, alors qu’ils disposent d’une procédure bien rôdée pour retrouver leur lecture et leur écriture : compter-numéroter les cases de la file numérotée.
Rappelons encore une fois cette citation des époux Fareng qui date de 1966 : « … (le comptage-numérotage) fait acquérir à force de répétitions la liaison entre le nom des nombres, l’écriture du chiffre, la position de ce nombre dans la suite des autres, mais elle gêne la représentation du nombre, l’opération mentale, en un mot, elle empêche l’enfant de penser, de calculer ». En fondant l’apprentissage de la lecture-écriture des nombres sur la seule répétition, plutôt que de l’expliquer par les décompositions à l’aide de 10, le pédagogue voit ses élèves apparemment réussir, mais, sur le long terme, cette pseudo réussite (réussite sans compréhension) fait obstacle à l’entrée dans le calcul.
L’effet délétère d’un apprentissage behavioriste de l’écriture des numéros après 20.
De même, lorsque les élèves découvrent les écritures 20, 21, 22, 23… 30, 31… dans le contexte d’une file numérotée, ils remarquent très vite que lorsque le numéro qui figure dans une case commence par un « 2 », c’est-à-dire lorsqu’il est du type « 2§ », il faut le lire « vingt-§ » (22 se lit « vingt-deux », 23 se lit « vingt-trois », 24 se lit « vingt-quatre », etc.). Idem pour les écritures qui sont du type « 3§ » mais avec « trente », etc.
Encore plus facilement qu’avec les écritures chiffrées après 10, les élèves apprennent ainsi à résoudre l’une des principales tâches scolaires : lire et écrire les numéros à deux chiffres à partir de 20. Et ils le font sans aucune référence aux propriétés numériques qui fondent ces écritures, celles d’un changement d’unité de compte lors d’un dénombrement : quand une collection est trop grande, plutôt que de dénombrer des unités simples, on gagne du temps en dénombrant des dizaines ; et c’est possible parce que l’écriture et la désignation orale des nombres utilisent cette grande unité de compte qu’est la dizaine : «vingt-trois » s’écrit 23, en juxtaposant un « 2 » et un « 3 », parce que la quantité correspondante se décompose en 2 dizaines et 3 unités.
Dans le cadre d’un enseignement qui n’est pas seulement behavioriste, la régularité verbale et l’écriture des nombres après 10 ayant une explication conceptuelle (les décompositions-recompositions à l’aide de dizaines), le pédagogue doit s’appuyer sur cette explication dès la première rencontre à l’école avec le nom et l’écriture de ces nombres. Le risque, sinon, est que l’enfant s’enferme dans la représentation des quantités à l’aide d’une suite de numéros. Dans une progression basée sur la compréhension, l’enseignant doit progresser plus lentement mais favoriser d’emblée l’appropriation des propriétés conceptuelles.
En effet, la principale difficulté qui surgit lorsque l’école valorise l’enseignement des stratégies de comptage-numérotage de bas niveau plutôt que de valoriser d’emblée les stratégies de décomposition-recomposition, est que les élèves les plus fragiles s’enferment dans leur emploi. Pour ces élèves, le changement de stratégie est couteux et, le plus souvent, ils en perçoivent mal l’intérêt. C’est le cas par exemple de cet élève à qui il est proposé le problème suivant (évaluation de fin de CE1) : « À la récréation, Dimitri joue aux billes. Au début de la partie il possède 37 billes. À la fin, il a 72 billes. Combien a-t-il gagné de billes ? ».
Il le résout ainsi :
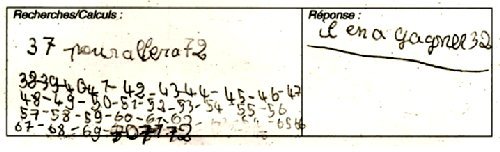
Examiné sous l’angle théorique, il apparait que ce type de résolution se fonde sur un usage des numéros comme s’il s’agissait de billes. En effet, l’élève sait ce qu’est une quantité de 37 billes : c’est celle que l’on forme en comptant 123456… 35, 36, 37. L’énoncé dit que le garçon évoqué dans le problème, Dimitri, gagne des billes. Lesquelles ? Bien évidemment la 38, la 39, la 40, la 41, la 42… jusqu’à la 72. L’élève écrit tous ces numéros et il compte ces numéros comme s’il s’agissait de billes. Il se trompe mais la stratégie aurait pu le conduire à la réussite. Alors pourquoi l’usage de ce type de stratégie ne doit jamais être favorisé à l’école ?
On remarquera que l’élève n’a besoin d’aucune connaissance conceptuelle concernant l’écriture des nombres : lorsqu’il écrit 40, 50, 60, 70, ce sont des numéros en tout point analogues aux autres. Il n’a pas besoin de savoir que 37=30+7, que 72=70+2… , il ne fait appel à aucune décomposition. Savoir compter-numéroter lui suffit. Malheureusement, lorsque l’usage de ce type de stratégie est installé, il est extrêmement difficile au pédagogue de favoriser l’accès à un niveau supérieur de résolution, celui d’une résolution arithmétique où l’enfant utilise des relations entre les nombres.
Cela renvoie à un phénomène très général : on a plus de mal à changer d’idée qu’à en adopter une nouvelle non installée. Les enfants dont la flexibilité cognitive n’est pas le point fort paient très cher les succès à court terme résultant d’une représentation des quantités par des suites de numéros. Parmi les nombreux résultats scientifiques qui vont dans ce sens, on peut renvoyer à ceux qui sont cités dans la synthèse de l’INSERM consacrée aux élèves en grande difficulté avec les nombres de manière durable : il y a consensus pour considérer qu’il s’agit d’enfants enfermés dans l’usage du comptage-numérotage et qui ne mémorisent pas de relations numériques.
Mieux vaut, au CP, enseigner l’écriture des nombres plus progressivement, voire moins loin, que de l’enseigner en s’appuyant sur un comptage-numérotage. Les concepteurs des repères de progressivité 2018 ont-ils essayé de réfléchir deux secondes aux raisons qui expliquent qu’un grand nombre de pays ne font étudier que les 20 premiers nombres au CP : Belgique, Finlande, Norvège, Suède… ?
Au CE1, des progressivités complètement différentes en 2015 et 2018
Comparons de même les repères de progressivité qui figurent dans les programmes de CE1 en 2015 et en 2018 respectivement :
• En 2015, on lisait : « Au CE1, un temps conséquent est consacré à la reprise de l’étude des nombres jusqu’à 100, notamment pour leur désignation orale et pour les stratégies de calcul mental ou écrit. Parallèlement, l’étude de la numération décimale écrite (centaine, dizaines, unités simples) est étendue par paliers, jusqu’à 200, puis 600 et éventuellement 1000 »
• En 2018, on lit : « (au CE1,) dès le début de l’année, les élèves poursuivent l’étude de la numération décimale en travaillant avec des centaines. »
Là encore, les repères 2015 constituaient une mise en garde : attention, au CE1 l’étude des nombres à 3 chiffres doit se faire progressivement, il faut se garder de vouloir aller trop vite. Il est important d’étudier les 200 premiers nombres avant d’aller au-delà. Les professeurs de CE1 ont même le droit de n’enseigner que les 600 premiers nombres à ce niveau de la scolarité. Comment expliquer cette mise en garde contre une progression trop rapide ?
Une propriété conceptuelle fondamentale des nombres à 3 chiffres
Au-delà de 100, pour accéder à la compréhension d’un nombre comme 127, il ne suffit pas de savoir que c’est 1 centaine, 2 dizaines et 7 unités, parce qu’il faut de plus savoir que c’est 12 dizaines et 7 unités. Pour comprendre l’importance d’une telle connaissance conceptuelle, il suffit de penser au calcul de 31 x 4, par exemple, dont le résultat est immédiat lorsqu’on sait que 4 fois 3 dizaines, 12 dizaines, c’est 120 (le résultat est 124). Ou encore à la division de 127 par 10 dont, là encore, le quotient et le reste s’obtiennent immédiatement lorsqu’on a cette connaissance (127, c’est 12 dizaines et encore 7, c’est-à-dire 12 fois 10 et il reste 7). Ou encore à la division posée de 127 par 3 (on ne peut pas partager 1 centaines en 3, on partage donc… les 12 dizaines de 127).
L’élève qui n’a pas ce type de connaissances est obligé d’apprendre un grand nombre de règles, les règles de « retenues » dans les opérations posées notamment. Ces règles semblent sans rapport les unes avec les autres alors qu’elles ont toutes le même fondement : une compréhension approfondie de la numération décimale. Or, en mathématiques, comprendre c’est construire un réseau de connaissances conceptuelles qui fondent les savoir-faire. Dans un apprentissage raté, ces savoir-faire résultent d’un catalogue de règles sans justifications et sans liens entre elles. Faute de compréhension, c’est-à-dire de connaissances conceptuelles, les élèves en difficultés sont submergés par le nombre de règles qu’on essaie de leur inculquer.
Alors pourquoi, au CE1, commencer par enseigner l’écriture des 200 premiers nombres après avoir révisé les propriétés des 100 premiers, comme cela était recommandé en 2015 ? Parce qu’il est plus facile d’enseigner que 127 c’est 12 dizaines et encore 7 que d’enseigner que 827 c’est 82 dizaines et encore 7. Pour apprendre que 127 c’est 12 dizaines et encore 7, la manipulation d’un matériel de numération est encore possible, avec 827 c’est une autre affaire. Avec du matériel de numération, les 12 dizaines de 127 se reconnaissent assez facilement comme 10 dizaines et encore 2 dizaines alors que 82 dizaines ne se reconnaissent pas comme 80 dizaines et encore 2 dizaines, sauf à savoir que 80 dizaines (800) c’est 8 dizaines de dizaines (8x10x10). Peu d’élèves de CE1 le savent.
Remarquons de plus que les repères de progressivité de 2015, laissaient la possibilité de n’enseigner les nombres que jusqu’à 600 au CE1. L’idée était, lorsqu’on décompose un nombre à 3 chiffres en dizaines et unités, d’éviter la difficulté résultant de l’irrégularité langagière des nombres après 69. Il est évidemment très difficile de comprendre que sept-cents c’est soixante-dix dizaines, par exemple.
Les recommandations 2018 font fi de toutes ces considérations : les concepteurs de ces repères de progressivité pensent que, dès le début de l’année les élèves doivent apprendre de façon behavioriste que, face à une écriture telle que 732, ce numéro se lit facilement de la façon suivante : il convient d’isoler le chiffre de gauche « 7 » (sept), puis de lui accoler « cent » (sept-cents) et, enfin, de prolonger ce que l’on dit en lisant le nombre formé par les deux derniers chiffres (sept-cent-trente-deux). Et ils espèrent que les mêmes élèves, plus tard, se compliqueront la vie à apprendre que 732 c’est 73 dizaines et encore 2. C’est totalement irréaliste. Ont-ils essayé de réfléchir deux secondes aux raisons qui expliquent qu’un grand nombre de pays ne font étudier que les 200 premiers nombres au CE1 : Allemagne, Belgique, Finlande, Norvège, Pays Bas, Suède… ?
Les recherches scientifiques confortent les choix de 2015, pas ceux de 2018
De nombreux résultats de recherche ont déjà été évoqués dans ce texte : recherche de la DEPP, synthèse de l’INSERM sur la « dyscalculie », comparaison internationale des différents programmes scolaires, histoire des discours et des pratiques pédagogiques…
La neuropsychologie cognitive est loin d’être capable d’étudier l’appropriation par les enfants des propriétés conceptuelles des nombres et des opérations arithmétiques. Aujourd’hui, l’imagerie cérébrale est un outil qui ne le permet pas. En revanche, en psychologie cognitive, les propriétés conceptuelles sont de plus en plus souvent mises en avant. Ainsi Elisabeth Spelke, dans une synthèse sur les connaissances disponibles concernant l’appropriation des nombres par l’enfant, affirme : « (I) reject the thesis that counting is central for number » et elle insiste sur le rôle majeur de l’expression verbale des décompositions-recompositions. Elisabeth Spelke est professeur de psychologie à Havard et elle est l’une des principales théoriciennes du domaine.
En didactique des mathématiques, récemment, trois thèses ont été soutenues portant sur la compréhension de l’écriture des nombres à plusieurs chiffres : celles de Christine Chambris (2008), Éric Mounier (2010) et Frédérick Tempier (2014). Quatre tâches sont principalement utilisées dans ces thèses afin d’évaluer le niveau de compréhension de l’écriture des nombres chez les élèves :
• Une tâche de lecture-écriture : passage du nom du nombre à son écriture chiffrée ou inversement.
• Une tâche de quantification : face à 45 unités, par exemple, pour dire combien il y en a, l’enfant va-t-il les compter 1 à 1, va-t-il faire des groupements de 10 puis compter 10, 20, 30, 40, 45 ou bien va-t-il dénombrer d’abord les groupes de 10 : il y en a 4 donc 40 unités et encore 5, 45 ?
• Une tâche où il s’agit d’écrire le nombre correspondant à une décomposition décimale non canonique : « 13 dizaines + 8 » ou bien « 4 centaines + 13 dizaines »
• Des résolutions de problèmes dont la solution numérique s’obtient assez directement lorsqu’on sait, par exemple, que 138 = 13 dizaines + 8 : « On dispose de 138 gâteaux et on veut former des paquets de 10 gâteaux. Combien de paquets peut-on faire ? ».
Les résultats sont très nets : la tâche de lecture-écriture est très bien réussie (sauf au CP et début CE1 pour les nombres entre 70 et 99, évidemment), celle de dénombrement voit un grand nombre d’élèves enfermés dans la procédure de comptage : 10, 20, 30, 40, 45 et qui n’accèdent pas à celle consistant à dénombrer des dizaines (il y a 4 dizaines et 5 unités, donc 45 unités). Les deux dernières tâches (décomposition décimale non canonique et résolution de problèmes) sont particulièrement mal réussies pendant tout le cycle 2. Ces résultats sont tout à fait cohérents avec l’analyse proposée dans ce texte : un apprentissage béhavioriste de la lecture-écriture des numéros, celui qui était recommandé entre 1986 et 2015, permet la réussite aux tâches de transcodage, il permet de quantifier une quantité en raccourcissant un comptage 1 à 1 par un comptage de 10 en 10, mais dès qu’une tâche fait appel aux connaissances conceptuelles qui expliquent l’écriture des nombres, elle est échouée. Or, seules ces connaissances conceptuelles assurent la réussite scolaire sur le long terme.
Une consultation biaisée
Rappelons d’abord que la rédaction du programme 2015 s’est effectuée dans de bonnes conditions n’ayant rien à voir avec celles du projet actuel : pour chaque cycle, le CSP a mis en place des commissions, celles-ci ont procédé à des auditions, elles ont constitué des sous-commissions de quelques personnes qui se sont particulièrement intéressées à une ou deux disciplines, ces sous-groupes ont fait appel à des personnes extérieures (dont l’auteur de ces lignes) pour aider à la rédaction du projet, etc. A chaque étape, la composition des différentes commissions était publique, de même que les contributions des principaux acteurs qui se sont engagés dans cette élaboration.
Au terme de ce processus, et concernant les mathématiques au cycle 2, des points d’accord fondamentaux ont émergé, notamment le choix de mettre en avant l’usage de stratégies de décomposition-recomposition lors des premiers apprentissages numériques, lors de l’apprentissage de l’écriture des nombres et du travail avec les grandeurs. Répétons-le : ces programmes rompaient avec l’approche des nombres par le comptage-numérotage qui était celle des programmes entre 1986 et 2015. Aboutir à un tel consensus était loin d’être évident. Le programme 2015 donnait l’espoir d’une future baisse de l’échec scolaire en mathématiques parce qu’il renouait avec la culture pédagogique qui était celle de l’école française à une période où les écoliers calculaient encore bien.
Aujourd’hui, des personnes anonymes proposent tout simplement de revenir aux programmes, aux pratiques pédagogiques et à la progressivité qui, très vraisemblablement, sont responsables de l’effondrement des performances en calcul des écoliers français. De nombreuses recherches dans des domaines différents, menées par des chercheurs différents, étayent ce diagnostic.
Rappelons les questions posées dans le cadre de la consultation actuelle :
1. Selon vous, quels sont les points forts des repères annuels de progression et des attendus de fin d’année?
2. Selon vous, quels sont les points à améliorer?
3. Comment envisagez-vous de mettre en œuvre les repères annuels de progression et les attendus de fin d’année en classe?
4. Comment les repères annuels de progression et attendus de fin d’année peuvent-ils contribuer au travail d’équipe ?
Le moins que l’on puisse dire est que ces questions n’incitent guère à remettre en cause de fond en comble la progressivité qui est proposée, comme cela vient d’être fait. Répondons brièvement à la question 4 : pour favoriser la réussite de leurs élèves, les professeurs d’un équipe d’école devraient se réunir et se livrer à une critique sans concession de la proposition d’un retour aux programmes de la période 1986-2015. Ceci fait, on n’imagine guère qu’ils décident d’adopter la progressivité avancée dans le document proposé à la consultation. Et s’ils le décident malgré tout, ils le feront en connaissance de cause.
Rémi Brissiaud
Maitre de Conférences honoraire de psychologie cognitive
Membre du conseil scientifique de l’AGEEM
Bibliographie
Brissiaud, R. (2013) Apprendre à calculer à l’école – Les pièges à éviter en contexte francophone. Paris : Retz
Canac, H. (1955) L’initiation au calcul entre 5 et 7 ans. In F. Brachet, H. Canac & E.
Chambris, C. (2008) : Relations entre les grandeurs et les nombres dans les mathématiques de l’école primaire. Évolution de l’enseignement au cours du 20ème siècle. Connaissances des élèves actuels. Thèse Université Paris 7.
Ermel (1977) Apprentissages mathématiques à l’école élémentaire – cycle préparatoire. Paris : Sermap-OCDL
Fareng R. & Fareng, M. (1966) Comment faire ? L’apprentissage du calcul avec les enfants de 5 à 7 ans. Paris, Fernand Nathan.
Inserm (2007) Dyslexie, dysorthographie, dyscalculie. Bilan des données scientifiques. Paris : les éditions Inserm.
Ministère de l’Éducation Nationale (1986) L’école maternelle, son rôle, ses missions. CNDP
Mounier, E. (2010) : Une analyse de l’enseignement de la numération au CP. Vers de nouvelles pistes. Thèse Université Paris 7.
Tempier F. (2013) La numération décimale de position à l’école primaire. Une ingénierie
didactique pour le développement d’une ressource. Thèse Université Paris 7.
Rocher T. (2008) Lire, écrire, compter : les performances des élèves de CM2 à vingt ans d’intervalle 1987-2007. Note 08.38 de la DEPP ; décembre 2008.
Savard, C. (1940) Pages choisies de pédagogie contemporaine, Paris : Delagrave.
Spelke E. (2017) Core Knowledge, Language, and Number. Language Learning and Development, 13- Issue 2: The Representation of Number: Origins and Development











