Serge Petit : Quelques éléments d’analyse des évaluations de CE1

Les évaluations de CP et de CE1 sont parues, elles suscitent bien des réactions d’ordre politique, d’ordre syndical, d’ordre pédagogique et posent de nombreuses questions sur leur pertinence. Mon propos est ici d’effectuer une rapide et très incomplète analyse de l’évaluation proposée en mathématiques en début de CE1.

Les programmes de mathématiques du cycle 2, clarifiés et ajustés parus au BO du 26 juillet 2018 ne font plus état des strates CP, CE1 et CE2 pour ce qui concerne l’enseignement des mathématiques au cycle 2. Les attendus sont des attendus de fin de cycle en termes de compétences et de connaissances. Les équipes pédagogiques, dans le respect absolu des programmes disposent de trois années scolaires pour permettre à tous les élèves d’atteindre les objectifs de fin de cycle. Les approches de l’enseignement des mathématiques peuvent considérablement varier d’une équipe de cycle à une autre. Il est donc assez paradoxal qu’une évaluation uniforme, indépendantes des choix pédagogiques des enseignants, soit imposée par le ministère. Laissons de côté ce point pourtant essentiel pour nous interroger rapidement sur les évaluations elles-mêmes.

Comme nous venons de le voir, ces évaluations ne sont compatibles ni avec l’esprit, ni avec les textes des programmes revus. Le cœur de cible des enseignements du cycle 2 est constitué du Lire, écrire et comprendre, ces apprentissages devant être mis en place dans toutes les disciplines. Or les élèves évalués en début de CE1 n’ont aucun texte à lire ni à écrire en mathématiques. Quand on connait les difficultés qu’éprouvent les élèves en résolution de problèmes, qui doivent « être au centre de l’activité mathématique »[1], dont beaucoup sont donnés sous forme de textes, on peut raisonnablement penser que les évaluations n’ont pas pour objet de mesurer les acquis fondamentaux des élèves dans le domaine de la maitrise de la langue dans les disciplines.

La compréhension (mais ce terme est-il toujours d’actualité dans les sphères ministérielles ?) du système de numération de position n’est pas testée. Qu’est le sens du 3 dans l’écriture 53, qu’est le sens du 5 dans cette même écriture, qu’est le sens du 0 dans l’écriture 10, celui du 1 dans cette même écriture ? Il se pourrait que le ministère, n’évaluant pas explicitement ces connaissances en fin de première année du cycle 2, considère que les élèves disposent de trois années pour bien comprendre et maitriser le sens du système positionnel de désignation des nombres. Cette conjecture serait en cohérence avec l’absence de calculs posés (additions, soustractions) au profit du calcul en ligne, conformément à l’excellent document figurant sur Eduscol, Le calcul en ligne au cycle 2. Ce dernier document fait état du sens de l’égalité, acquisition fondamentale, souvent enseignée à tort comme l’indication du déclencheur d’un calcul. Une indication sur la maitrise de cette relation fondamentale entre désignations d’un même nombre aurait pu être utile aux enseignants de cycle 2. Hélas, elle n’est pas testée. Il y avait pourtant à ce sujet bien des activités de remédiation à suggérer, tout autant que pour une éventuelle méconnaissance du système positionnel de désignation des nombres. Cette évaluation semble donc passer à côté de compétences et de connaissances en cours d’apprentissage pour lesquelles certains enseignants auraient pu avoir besoin d’éclaircissement et certains parents d’une information précise.

On pourrait passer bien du temps à analyser cette évaluation en regard des programmes et de leurs priorités, des attendus de fin de cycle. Passons à un autre point de vue, interne à l’évaluation elle-même et interrogeons-nous à propos de quelques consignes et du travail attendu des élèves.

Une première remarque s’impose, les consignes sont données à l’oral et uniquement à l’oral, ne permettant pas aux élèves de se rattraper en cas de perte de mémoire, ne leur permettant pas non plus d’exercer leurs compétences de lecteurs dans le sens (abandonné ?) de comprendre. Ces consignes sont toujours précédées d’un exemple, suivi de l’affirmation « maintenant que vous avez compris ». Cette manière de procéder semble digne des pédagogies explicites[2]… et comment l’enseignant peut-il supposer qu’après avoir observé un exemple, tous les élèves ont compris. Nous verrons d’ailleurs que même un adulte, de surcroit spécialiste des mathématiques peut ne pas comprendre une consigne donnée, malgré l’exemple.

L’évaluation en mathématiques en CE1 comporte neuf exercices dont nous proposons une très rapide analyse.

Exercice 1 :

La « compétence associée » à cet exercice est libellée « Lire des nombres ». Or, à ce que je sache, personne n’a jamais vu de nombre, personne ne peut donc lire un nombre. Pire, la consigne donnée aux élèves est « Entoure le nombre X ». Comment peut-on entourer un nombre ? La tâche est impossible, car les nombres sont des concepts, elle est pourtant demandée par des évaluations réalisées par des équipes de spécialistes qui conseillent le ministre. Curieusement, la description de l’activité fait le distinguo entre objet ou concept et leurs désignations « Associer les noms de nombres à leur écriture chiffrée ». Il faut cependant remarquer que tout nombre a une multitude de désignations chiffrées, mais dans le contexte de cette évaluation, il n’y en a qu’une seule possible par ligne, d’où, vraisemblablement le singulier. Une consigne correcte n’aurait pas été bien difficile à formuler pour des élèves ayant suivi une année d’enseignement durant laquelle on ne confond pas les nombres et leurs diverses désignations.

Exercice 2 :

Cette fois-ci, la compétence semble correctement libellée. L’activité fait réfléchir : « Calculer mentalement des additions… ». Calculer est un terme générique qui peut signifier additionner, soustraire. Une addition est un calcul. Il convient de l’effectuer…, mais ne pinaillons pas. Cet exercice a tout à fait sa place dans une évaluation de début de CE1. Une indication dans le texte prête à sourire : « Vérifier. Si un élève n’a pas entouré la bonne réponse, s’assurer qu’il a bien compris la consigne même s’il a fait une erreur de calcul. Sinon, réexpliquez-lui sans lui donner la réponse. » Amusant, non ? Comment un enseignant peut-il durant les dix secondes laissées aux élèves pour chaque calcul à la fois vérifier que tous les élèves ont entouré la bonne réponse et réexpliquer à chacun des élèves n’ayant pas entouré cette dernière ?

Maintenant que nous avons compris, passons à l’exercice 3.

Exercice 3 : la catastrophe !

La consigne est correctement libellée et porte sur une activité essentielle au cycle 2, à savoir la représentation des nombres entiers : « représenter un nombre entier ». D’ailleurs, le verbe représenter est l’un des six verbes qui gouvernent les activités mathématiques. L’exercice semble davantage porter sur la représentation d’une décomposition additive des nombres, qui représente bien évidemment un nombre.

L’exemple qui doit permettre à tous de comprendre est constitué de trois dominos à deux cases, dans chacune des cases sont dessinés des cercles, pour un premier domino, des croix pour le deuxième et des dièzes pour le troisième. Il s’agit « d’entourer tous les dominos qui font le nombre indiqué en haut de la page ». L’exemple porte sur le nombre désigné par le mot trois.

La consigne est la suivante : « Sur cette page, vous allez entourer tous les dominos qui font le nombre indiqué en haut de la page : sur la première page de l’exercice, c’est le nombre 7 . Attention parfois le domino est fait de deux parties, parfois il est fait avec trois parties. Il faut additionner tout ce qui se trouve dans toutes les cases du domino. Si ce sont des petits dessins, il faut tous les compter puis entourer si ça fait le nombre demandé ».

Les élèves disposent de deux minutes pour entourer un maximum de dominos. Sur la page avec entête 7, figurent 21 dominos dont six avec trois cases. Idem sur la page à entête 13.

Quelques exemples et interrogations

Exemple 1 :

Cet exemple est clair. Il faut entourer le premier domino qui représente bien sept objets en tout.

Exemple 2 :

Cet exemple, qui figure aussi sur la page dont l’entête est 7, est bien moins clair. Combien d’objets en tout dans ces trois dominos : deux par domino. Les objets sont des dessins, aussi appelés chiffres qui ne désignent rien hors contexte. Si nous revenons à la consigne : « il faut additionner tout ce qui se trouve dans toutes les parties du domino », l’élève peut comprendre qu’il faut additionner les nombres représentés par ces chiffres. Bien sûr la consigne a prévu : « Si ce sont des petits dessins, il faut tous les compter puis entourer si ça fait le nombre demandé ». Mais cette consigne ne dit rien si ce ne sont pas des « petits dessins » !

Exemple 3 :

Cet exemple, qui figure sur la page dont l’entête est 13, est encore, si c’est possible, plus problématique. Comment définir les « petits dessins » ? Y a-t-il deux mains, un quadrilatère et deux disques ? Dans ce cas, il ne faut pas entourer le « trimino » puisqu’il représenterait le nombre désigné par 5. Y a-t-il dix doigts, un quadrilatère et deux disques ? Dans ce cas, il faudrait entourer le « trimino » et c’est peut-être la réponse attendue. Mais se pose alors la manière de définir les « petits dessins ». L’élève doit-il observer des particularités de certains dessins ? Si cette dernière conjecture prévaut, il faudrait peut-être dire que le quadrilatère représente quatre traits ou quatre pointes… tout comme, dans le premier exemple, chaque étoile (à droite) représenterait alors cinq pointes… et tout l’exercice tombe à l’eau.

Tout se passe comme si les experts ayant conçu ces évaluations éprouvaient des difficultés avec les notions sémiotiques fondamentales et étaient ignorants de travaux comme ceux de Raymond Duval[3] portant notamment sur les registres sémiotiques de représentation.

Pourtant : « L’implication du CSEN permet de bénéficier des dernières avancées de la recherche en vue d’accroître l’efficacité de ces évaluations et ainsi de mieux répondre aux besoins des élèves »[4] Il s’agit peut-être des dernières avancées qui ont tiré un trait sur celles qui précèdent.

Un tel exercice, si problématique, peu au clair sur les concepts en jeu, ne devrait pas trouver place dans une évaluation dont les enjeux sont présentés comme étant essentiels.

On peut remarquer de plus qu’aucun exercice ne permet de vérifier, compétence essentielle, que l’élève mobilise spontanément une décomposition additive de nombres pour résoudre un problème. L’aspect passif l’emporte dans tous les exercices sur l’activité de l’élève, exécutant.

Exercice 4 :

Cet exercice de comparaison de deux entiers permet de s’interroger sur une pratique constante dans ces évaluations, inscrire les performances des élèves dans une durée courte et chronométrée. Certains élèves ne sont-ils pas plus lents, mais pas moins efficaces en termes de réflexion, de créativité, que d’autres ? On dit même qu’un certain Einstein était un esprit lent à l’école…

Exercice 5 :

Il s’agit de résoudre des problèmes additifs, tout à fait à la portée des élèves lorsqu’ils sont écrits et que l’élève est obligé de lire et de comprendre un énoncé. Mais les énoncés sont lus. Pourquoi donner une telle priorité à l’oral alors que la maitrise de la langue écrite est un objectif fondamental du cycle 2 et que des observations de la capacité des élèves à lire et comprendre en autonomie serait essentielle ? L’élève fournit sa réponse en entourant une désignation chiffrée d’un nombre. Pourquoi ne pas profiter de la résolution d’un problème pour s’assurer qu’en mobilisant une partie des mots de l’énoncé l’élève est capable d’écrire une phrase lexicalement, grammaticalement et syntaxiquement correcte ?

Il est plus difficile à un élève (comme d’ailleurs à un adulte) de comprendre un énoncé de problème donnée oralement. Ce n’est pas pour rien que les programmes insistent tant sur le rôle de l’écrit pour penser. Cet écrit est un appui pour faciliter la résolution de problèmes. L’effet pervers de cette lecture oralisée avec possibilité de prise de note ne va-t-elle pas amplifier la tendance des élèves à se focaliser sur les nombres et à faire des opérations à partir de ces nombres sans chercher à comprendre l’énoncé, à se représenter la situation sous-jacente ?

Exercice 6 :

Exemple 1 :

Il s’agit d’ « associer un nombre entier à une position », c’est le type même d’exercices présentés sur eduscol[5]. Quand ces exercices portent sur la relation « … est entre… » et que le résultat peut se trouver par élimination de certaines propositions, il est tout à fait au niveau d’un début de CE1 et permet de vérifier des connaissances portant sur la relation d’ordre.

Exemple 2 :

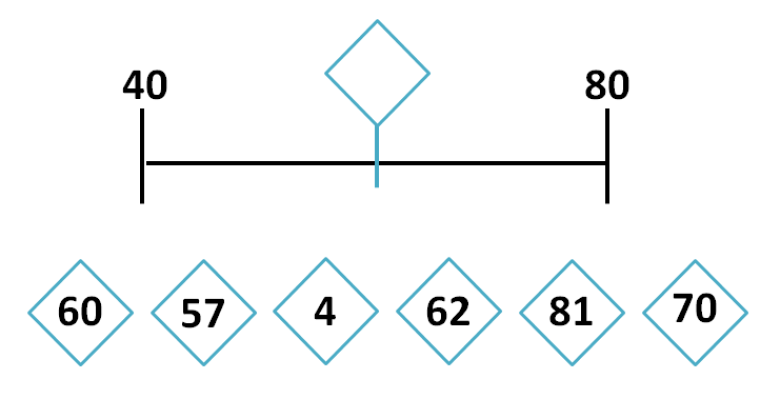
Par contre, quand ils concernent la représentation d’un nombre sur une droite graduée régulièrement et que les graduations ne sont pas indiquées, ils dépassent de beaucoup le début de CE1 comme c’est le cas sur les deux exemples ci-contre. Le premier exemple est toutefois plus facile a priori que le second par la perception du « milieu ». Dans un tel exercice, il conviendrait d’accepter, en début de CE1, les réponses 60 (celle attendue), mais aussi 57, 62 et 70. La différence de position entre 62 et 60 est imperceptible à l’œil. Faire des mathématiques serait-ce répondre au hasard ?

Dans le deuxième exemple, il conviendrait d’accepter les réponses 82 et 83 pour les mêmes raisons.

La droite graduée est certes fondamentale en mathématiques, mais elle se construit au fur et à mesure des apprentissages, comme outil de représentation des nombres, du CP au CM2 et encore bien après. Laissons, comme le prévoient les programmes, le temps aux élèves pour apprendre.

Nous restons curieux de voir comment le ministère va interpréter les réponses des élèves, de connaitre les consignes qu’il donnera aux professeurs de CP pour que les erreurs relevées ne se présentent plus et quelles aides il suggérera aux enseignants de CE1 à propos de ce type d’exercices. Il devra également justifier sa position devant les parents, partenaires de l’éducation.

Exercice 7 :

Cet exercice consiste à repérer dans une liste de six écritures chiffrées celle qui correspond au résultat d’un calcul à effectuer (sommes ou différences)., présenté en début de ligne Cet exercice est à la portée des élèves de début CE1, mais là encore : pourquoi leur demander de choisir dans une liste préétablie et ne pas les laisser écrire ? L’écriture deviendrait-elle un tabou en mathématiques ?

Ces deux pages de calcul dans lesquelles l’égalité est utilisée à chacune des quinze lignes aurait pu servir également à tester la conception que les élèves se font de ce concept fondamental en demandant de repérer des désignations additives ou soustractives des mêmes nombres. La non-maitrise de l’égalité étant un facteur majeur de difficulté des élèves à résoudre certains problèmes et surtout, en cycle 3, à effectuer des conversions de représentations de nombre entre désignations fractionnaires et désignations décimales car bien des élèves confondent nombres et désignations de nombres et imaginent donc qu’un nombre a une et une seule désignation possible.

Exercice 8 :

Cet exercice est un exercice de conversion de registre sémiotique. Des désignations de nombres sont lues par l’enseignant, les élèves doivent indiquer en chiffre la désignation canonique de ces nombres (désignations à deux chiffres). Bien évidemment, la consigne est « je vais vous dire des nombres », comme si les nombres pouvaient être dits ! La confusion entre nombres et désignations des nombres (représentation des nombres) est entretenue pas cet exercice.

On peut se demander ce que l’écriture 100 vient faire dans cet exercice, mais c’est sans doute pour connaitre la proportion d’élève connaissant cette écriture qu’il n’est pas nécessaire de rencontrer au CP.

Exercice 9 :

Cet exercice a vraisemblablement gêné les concepteurs car la compétence est libellée comme suit :

Compétence :

Se repérer dans l’espace en deux dimensions.(observer pour distinguer des figures géométriques)

La compétence invoquée ne figure pas dans le texte des programmes, ni de 2015, ni dans les programmes ajustés en juillet dernier. Quand les élèves doivent « se repérer », ils doivent le faire dans le monde en 3D, dans la réalité. Ils peuvent pour cela utiliser des représentations de l’espace. Ils peuvent aussi être amenés à « se repérer » dans un texte, dans un programme… mais il s’agit alors d’une tout autre acception du verbe.

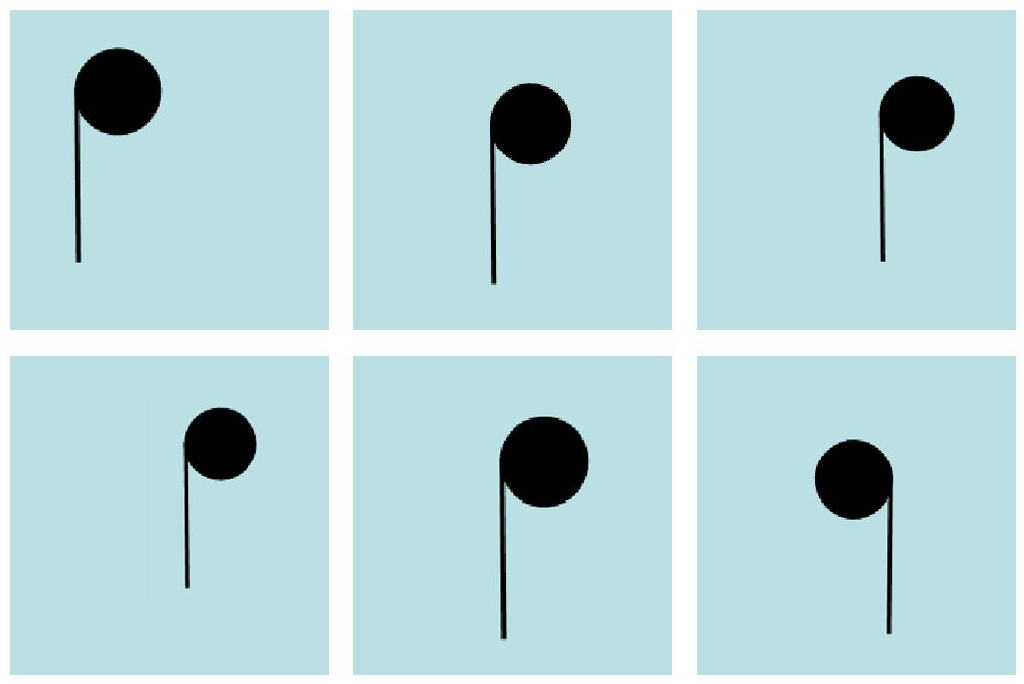Pourquoi donc avoir détourné une compétence ? Le détournement se lit dans la parenthèse « observer pour distinguer des figures géométriques ». Il ne s’agit pas du tout de repérage au sens défini par les programmes du cycle 2. La consigne donnée aux élèves : « Entourer l’intrus parmi 6 figures géométriques » ne correspond absolument pas à une activité où l’élève aurait à « se repérer » dans le monde, pas plus qu’à une activité qui consisterait à effectuer un repérage dans un plan.

Pour illustration, voir ci-contre un exemple d’exercice proposé :

Cet exercice est typique des tests de QI, il ne relève pas d’un enseignement spécifique au CP, son contenu ne figure pas aux programmes de l’école. On nous répondra qu’il s’agit de classer et de vérifier que l’élève est capable de mettre ensemble ce qui est pareil et de trouver ce qui ne l’est pas.

Alors, exercice de classement (tri ?) ou exercice de QI ? Nous le saurons quand le ministère aura publié les résultats. S’il s’agit d’un test de QI déguisé, est-il déontologiquement acceptable de le faire passer sans le consentement des adultes responsables des élèves ? Confiance !

Les évaluations CE1 ne permettent pas de mesurer les compétences et connaissances figurant dans les fondamentaux du cycle 2 comme la compréhension du système de numération de position, ou celle de l’égalité. Elles ne permettent pas d’évaluer les compétences des élèves en lecture et en écriture de la langue française, pourtant un des objectifs majeurs de l’école à ce niveau des apprentissages. Elles sont des évaluations passives, dans lesquelles les élèves n’ont jamais à mobiliser spontanément des connaissances ou compétences. Traduisent-elles alors ce que l’on attend d’un citoyen français ? La passivité ?

De plus, ces évaluations sont truffées d’erreurs ou de zones d’ombre qui permettent dès à présent de contester leur pertinence.

Les enseignants font face à une propagande politique qui veut laisser croire que toutes les décisions ministérielles sont fondées sur des recherches scientifiques, donc indiscutables et que quelques conseils ou décisions simplistes vont permettre la réussite de tous les élèves.

Il convient de manière urgente de suivre le conseil d’Olivier Houdé et, les professeurs des écoles, qui ne sont pas des moutons de Panurge, devraient « apprendre à résister aux automatismes de pensée lorsqu’ils sont simplificateurs et dangereux »[6].

Serge Petit

Professeur de mathématiques honoraire

IUFM d’Alsace