« Il n’y a pas que les maths qui comptent pour faire des maths. La langue aussi… » Ce titre est la conclusion d’un article de François Jarraud paru dans le Café du 29 septembre 2019 à propos d’une analyse des résultats obtenus à l’évaluation TIMMS par les élèves français de CM1. Je propose de l’illustrer par une recherche amorcée à l’automne 2019 en collaboration avec Annie Camenisch, maître de conférences à l’INSPE, Université de Strasbourg.
La recherche
Cette recherche portait sur la résolution de problèmes additifs de comparaison ou à transformations, les problèmes étant adaptés aux niveaux des élèves. Nous avions défini trois niveaux : CP, CE et CM, chacun de ces niveaux bénéficiant d’un protocole spécifique.
La crise sanitaire a empêché la recherche de se mettre en place au CP car il fallait attendre les environs du mois de mars pour que les élèves aient développé des aptitudes suffisantes en lecture et en écriture. Elle a débouché pour un peu plus de la moitié des élèves ayant rendus le test initial en CE1 (360/501), les trois quarts des élèves de CE2 (301/424), très peu d’élèves de CM1 (3/463) et peu d’élèves de CM2 (88/813).
La recherche au CE1
Le test initial CE1 comportait huit énoncés de problèmes additifs. Les quatre premiers étaient des problèmes à une comparaison, les quatre derniers, des problèmes à une transformation. Ce test a été suivi d’une proposition de travail encadrée par un protocole strict s’étalant sur huit semaines à raison de courtes séances quotidiennes. Le travail proposé aux enseignants portait sur la simulation de situations de comparaisons, la description orale et écrite de ces situations selon des points de vue différents (celui des observateurs, celui des acteurs). Il était proposé aux enseignants un travail spécifique en langue, travail portant sur la qualité sémantique (la phrase répond-elle à la question posée, que le résultat mathématique soit juste ou non), la qualité syntaxique de cette même phrase ainsi que sur les qualités orthographiques (orthographe lexicale et grammaticale). Ces points ont été observés à la fois dans le test initial et dans le test final de même nature que le test initial.
Nous n’ignorions pas l’importance des représentations graphiques diverses ou de la schématisation, mais nous avions réservé ce type de protocole aux CM1 et CM2, à l’exclusion du protocole CE. Il s’agissait donc d’étudier si un travail spécifique, ciblé et explicite portant sur la langue et lui seul pouvait améliorer les performances des élèves en résolution de ce type de problèmes. Il s’agissait aussi d’étudier la possibilité d’un transfert de compétences d’un travail portant exclusivement sur les problèmes de comparaison vers les problèmes à transformation. Il a donc été demandé aux enseignants de ne résoudre aucun problème à transformation durant tout le travail fixé par le protocole et de respecter celui-ci scrupuleusement.
Les élèves concernés provenaient de toutes les régions du territoire métropolitain et de tous types d’établissements (hors REP, REP et REP+).
Voici les résultats en mathématiques des 360 élèves de CE1 ayant été jusqu’au terme du protocole proposé.
On constate certes une progression des performances pour les problèmes à comparaison allant de 11% pour le plus facile à 67% pour le problème le plus difficile (analyse par congruence – en référence aux travaux de Raymond Duval, Sémiosis et pensée humaine, Peter Lang, 1995), ce qui peut paraître naturel puisque ces problèmes (et eux seuls) ont été travaillés en classe entre les deux tests espacés d’environ huit semaines. Mais on constate aussi une forte progression pour les problèmes de transformation, de 4% pour le plus facile à 103% pour le plus difficile (on dirait fortement non-congruent).
Il semble donc qu’il y ait eu transfert, non pas de l’utilisation d’un outil mathématique à appliquer, non pas d’automatismes, mais de compétences langagières ayant permis aux élèves de se forger une meilleure compréhension des énoncés de problèmes additifs (à une étape) en général, de développer une attitude plus réflexive et donc d’améliorer leurs performances en résolution de problèmes.
Ces élèves ont-ils amélioré, ce faisant, leurs performances en langue écrite ? Le tableau suivant fournit la comparaison des résultats entre les deux tests, toujours pour les mêmes 360 élèves de CE1 :
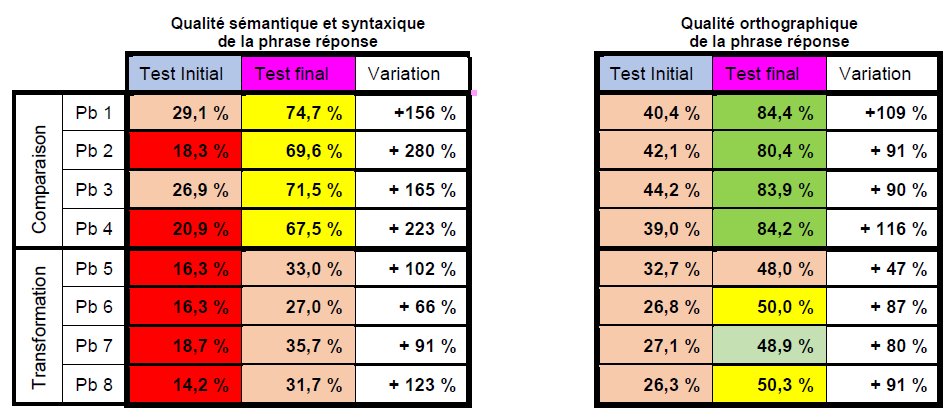
Ces résultats montrent une très forte progression relative à la qualité sémantique et syntaxique de la phrase réponse, à la qualité orthographique (lexicale et grammaticale) pour les problèmes à comparaison, seuls problèmes travaillés dans le protocole.
Si un transfert s’est effectué entre les apprentissages langagiers effectués à partir des problèmes à comparaison vers les apprentissages langagiers relatifs aux problèmes à transformation, il a engendré une moindre performance sur les qualités des productions écrites des élèves relatives aux problèmes à transformation.
Ce qui montre qu’il est nécessaire de prévoir des apprentissages langagiers spécifiques à chaque domaine des mathématiques, mais ne semble cependant pas pouvoir expliquer la différence de qualité orthographique des phrases réponses entre les problèmes de comparaison et les problèmes à transformation au test final.
On peut effectivement conclure du travail effectué qu’« Il n’y a pas que les maths qui comptent pour faire des maths. La langue aussi… ». Cette citation pourrait se symétriser « Il n’y a pas que le français qui compte pour apprendre la langue. Les maths aussi… ».
La recherche en CM1 et CM2
Les résultats très faibles enregistrés dès le retour des premiers tests initiaux de CM nous ont conduits à devoir modifier le protocole. De ce fait, le travail en classe s’est mis en place tardivement et, la crise sanitaire ayant fait son apparition, les classes engagées n’ont pas pu mener à bien cette recherche, sauf pour cinq classes représentant en tout 91 élèves sur les 1276 élèves de CM présents au test initial et dont nous avons les résultats.
Le test initial comportait deux énoncés communs avec les classes de CE (deux problèmes à une comparaison), auxquels s’ajoutaient deux problèmes à deux (donc trois) comparaisons et quatre problèmes à deux transformations dont un problème très difficile mêlant transformations et comparaisons, énoncé plagié d’un problème imaginé par Gérard Vergnaud et figurant dans l’ouvrage de R. Duval cité plus haut. Ce problème réussi par 6% (six pourcents) des 1276 élèves de CM et par 5% (cinq pourcents) de 1234 professeurs des écoles et cadres lors de conférences ou de formations, qui n’a pas fait l’objet d’un apprentissage systématique durant le protocole de travail, a été réussi au test final par plus d’un quart des élèves.
Le tableau suivant donne les résultats des seuls 91 élèves ayant bénéficié du protocole jusqu’à son terme. Les pourcentages de variation n’ont pas de sens compte tenu des faibles effectifs en jeu, ils sont simplement destinés à attirer l’attention sur l’hypothèse qu’un protocole de même nature que celui que nous avons mis en place pourrait faire croître les performances des élèves de façon assez significative.
Les difficultés des élèves ne résidaient pas dans les calculs, ne relevaient pas de concepts mathématiques trop fraîchement enseignés et encore mal assimilés puisque ces problèmes ne nécessitaient que la mobilisation d’outils mathématiques relevant du cycle 2 (additionner, soustraire, résoudre un problème à une comparaison, résoudre un problème à une transformation et leurs combinaisons). Les difficultés ne relevaient pas non plus des situations concrètes sous-jacentes aux énoncés, situations familières, mais bien de la représentation que pouvaient s’en forger les élèves. Cette représentation peut être mentale (mais on n’y a pas accès dans ce type de test), ou graphique ou langagière. Citons les programmes actuels de cycle 3 qui précisent que « D’une façon plus spécifique, l’élève acquiert les bases de langages scientifiques qui lui permettent de formuler et de résoudre des problèmes, de traiter des données. Il est formé à utiliser des représentations variées […] et à organiser des données de nature variée à l’aide de tableaux, graphiques ou diagrammes qu’il est capable de produire et d’exploiter. » Ces mêmes programmes préconisent de réaliser un « apprentissage explicite de la mise en relation des informations dans le cas de documents associant plusieurs supports (texte, image, schéma, tableau, graphique, etc.) » (p.14). On pourrait croire qu’il s’agit d’extraits des programmes de mathématiques. Non, ils figurent dans les programmes d’apprentissage de la langue, le dernier sous l’intitulé « Comprendre des textes ». Ce sont ces préconisations des programmes que nous avons appliquées.
Ce qui nous renvoie encore une fois à la citation du titre : « Il n’y a pas que les maths qui comptent pour faire des maths. La langue aussi… ».
Le protocole mis en place en classes de CM, qui a duré moins de deux mois en n’occupant qu’au maximum un tiers des horaires consacrés aux mathématiques (et encore, ces horaires auraient pu, pour une bonne partie, être déduits des horaires d’apprentissage de la langue, mais laissons de côté ces calculs d’épiciers qui n’ont de sens que pour les esprits qui cloisonnent les matières d’enseignement) a très nettement contribué à un accroissement remarquable des performances en mathématiques. Dois-je préciser que nous n’avons jamais, dans ces protocoles, fait appel au très fameux « diagramme en barres » ou à la « méthode en barre » ? Peut-être leur usage fournirait-il à lui seul des augmentations des performances de élèves bien supérieures, ce qui reste à démontrer.
Ce protocole a étroitement tissé apprentissages langagiers et d’autres outils de représentations sémiotiques (graphiques, diagrammes) allant jusqu’à élaborer des schémas avec les élèves, en réponse à des problèmes de représentations.
Les résultats en langue se sont améliorés de manière très nette en CM, avec des taux de réussites passant par exemple, pour le plus élevé de 7,7% à 74%, concernant la qualité sémantique et syntaxique de la phrase que l’élève doit écrire en réponse à un problème de comparaisons.
Quand nous enfonçons un clou, nous enfonçons un clou dira le lecteur qui rencontre pour la nième fois notre affirmation qu’il est nécessaire de travailler explicitement la langue en contextes mathématiques afin de mieux comprendre les énoncés de problèmes, afin, de manière plus générale de mieux comprendre les concepts mathématiques requérant bien souvent le recours à un lexique spécifique, à des syntaxes particulières, à des constructions de textes inhabituelles et peu fréquentés dans le français de la littérature, qu’il convient aussi d’articuler les registres de représentations.
Oui, comme d’autres, nous enfonçons un clou, mais nous désignons clairement ce clou, clou qui a été forgé à la main, en classes dans des expérimentation répétées, sur des publics variés et nous permettons de plus à celles et ceux qui le souhaite de s’en saisir et de l’enfoncer dans sa propre classe.
Vous avez des doutes, vous avez des élèves de CE2, CM1 ou CM2, vous souhaitez enfoncer ce clou : écrivez-nous à l’adresse sp.problemes@free.fr . Vous serez invité(e) à répliquer le travail réalisé en 2019-2020, travail de recherche qui a fait l’objet d’une communication au dernier colloque de la COPIRELEM en juin 2021 et dont le compte-rendu figurera dans les actes de ce colloque.
Conclusion
Un doute : nous ignorons si les neurosciences valident ce type de démarche qui trouve ses fondements dans des travaux de recherche européens en didactique des mathématiques, dans des travaux de chercheurs de notre continent en psychologie, mais aussi dans des travaux d’auteurs comme Jean-Charles Chabanne qui explicite la fonction heuristique d’écrits intermédiaire dans les disciplines scientifiques.
Le clou : travailler la langue en contexte mathématiques, pas seulement en résolution de problèmes, mais dans tous les domaines de l’enseignement des mathématiques, travailler de plus les différents modes de représentations, comme le précisent les programmes, est une nécessité absolue, à tous les niveaux scolaires, comme peut le suggérer la recherche très sommairement décrite ci-dessus.
La tenaille : chacune et chacun, à l’issue de sa propre expérience en classe, pourra librement s’emparer soit du marteau soit de la tenaille.
Serge Petit
P.S. clou, marteau et tenaille renvoient à une contribution du même auteur dans le Café pédagogique du jeudi 30 septembre 2021.
