PISA à l’épreuve des notes, Une autre lecture de la comparaison entre les pays

Les enquêtes internationales sur les acquisitions des élèves ont une histoire de plus de cinquante années dont l’origine est le fait de l’Institut de l’éducation de Hambourg, cette histoire a été particulièrement marquée par la création de l’IEA[1] en 1961 (Bottani, Vrignaud, 2005). Cet organisme, piloté par des chercheurs, a joué un rôle déterminant dans le développement des outils statistiques et plus généralement de la méthodologie utilisée dans ces grandes enquêtes comparatives dont la fréquence a augmenté au cours de ces dernières décennies. Plus récemment, l’OCDE[2] a donné une forte impulsion aux études internationales en éducation avec pour objectif le recueil d’éléments factuels et réguliers sur les systèmes d’enseignement en vue d’instruire les politiques éducatives. L’enquête PISA[3] a été lancée par l’OCDE en 2000 en bénéficiant de l’engagement des décideurs politiques dans ce programme international d’évaluation des compétences des élèves. Cette opération de très grande ampleur concerne à présent un nombre important de pays (65 pays ont participé en 2009 et 67 pays en 2012) et des moyens financiers substantiels sont mobilisés pour la réalisation des différentes étapes du programme. En outre, la richesse des informations collectées sur les élèves et les établissements, la dimension cyclique de l’enquête administrée tous les trois ans dans trois domaines de compétences (compréhension de l’écrit, culture mathématique et culture scientifique) sont autant d’éléments qui ont permis une large exploitation des résultats et qui ont contribué par ailleurs à la popularité de PISA.

Pour les chercheurs en éducation, les données PISA constituent une base de travail précieuse et elles donnent lieu à de nombreuses exploitations secondaires qui produisent des analyses originales et pertinentes sur l’efficacité, l’efficience et l’équité des systèmes éducatifs, mais aussi sur des aspects plus didactiques liés aux contenus des items (Rey, 2011). Ces exploitations scientifiques des données de PISA ont réellement contribué à obtenir une vision renouvelée des systèmes éducatifs (Olsen, Lie, 2006) en mettant aussi en évidence des typologies de pays aux organisations et aux résultats variés (Mons, 2008). La dimension comparative peut alors être perçue par la communauté des chercheurs comme une source de richesse par rapport à des analyses effectuées uniquement dans un cadre national (Duru-Bellat, Mons, Suchaut, 2004). Au final, l’atout essentiel du programme PISA est bien de nourrir et d’enrichir les débats politiques et sociaux sur l’école dans un grand nombre de pays. Les responsables des politiques éducatives font en effet systématiquement référence aux conclusions des analyses menées dans le cadre de PISA et les médias leur donnent une large place, notamment lors de la publication des résultats. Ainsi, dans certains pays, comme en Allemagne, l’impact de PISA en 2000 a été un véritable choc qui a donné lieu à de nombreuses publications dans la presse[4]. Dans d’autres pays comme la France, et au même moment, les réactions ont été plutôt discrètes lors de la publication du classement international.

Bien sûr, PISA n’échappe pas à certaines critiques. Une première, très générale, concerne le choix d’un âge pour la population d’élèves visée : en l’occurrence celui de 15 ans ne confère pas à l’échantillon la représentativité d’un niveau scolaire particulier dans certains pays (la France notamment), les élèves testés sont scolarisés, soit dans le secondaire inférieur, soit dans le secondaire supérieur, alors que ce n’est pas le cas dans les pays qui ont recours à la promotion automatique, comme la Finlande ou la Suède par exemple (Grenet, 2008). Mais les débats autour de la validité de PISA concernent surtout l’aspect de la mesure des acquis des élèves. Ainsi, les biais culturels, dont la présence est toujours possible dans ce type d’enquêtes, ont été évoqués et sont à mettre en relation avec le nombre important de langues concernées. La question de la formulation des items composant les épreuves et des modalités de correction a alors été posée (Robin, 2002). Certains chercheurs se sont aussi interrogés sur la conception de la littératie telle qu’elle est envisagée dans les épreuves PISA (Bautier, Crinon, Rayou, Rochex, 2006). Enfin, et plus largement, c’est le concept théorique de compétence qui peut même être remis en cause avec l’argument selon lequel PISA définit les compétences comme une réalité objective et autonome alors que celles-ci sont en fait le produit d’un modèle de mesure (Vrignaud, 2006).

Cette critique majeure sur la définition des compétences mobilisée dans PISA est à prendre en compte au regard de l’objectif de l’OCDE qui souhaite, à travers cette enquête, répondre à la question suivante : « Dans quelle mesure les jeunes adultes sont-ils prêts à relever les défis de demain ? » (OCDE, 2004, p. 7). Cette interrogation sur la nature des compétences est bien au cœur d’une problématique qui concerne le domaine scientifique, mais aussi la sphère politique. Le fait que PISA se démarque volontairement des connaissances figurant dans les programmes scolaires peut en effet avoir probablement une incidence sur l’interprétation des résultats en termes de palmarès entre pays ou régions : le classement des pays serait-t-il le même avec des épreuves plus proches des contenus scolaires ? L’intérêt du public est en revanche bien éloigné de ces préoccupations théoriques et méthodologiques, il se limite bien souvent au seul classement des pays, laissant le soin aux experts du domaine d’effectuer la lecture approfondie des documents volumineux publiés par l’OCDE et des rapports nationaux qui sont produits à la suite. Il existe alors un risque bien naturel que les interprétations soient succinctes, voire même parfois erronées (Grenet, 2008), ne permettant pas d’apporter les nuances nécessaires associées à la complexité de la méthodologie mise en œuvre dans l’enquête. Des efforts de pédagogie sont pourtant réalisés dans les documents de synthèse publiés par l’OCDE et par les pays participants pour fournir les éléments précis permettant une interprétation adéquate des résultats, notamment en ce qui concerne les scores moyens calculés pour chaque pays. Ainsi, l’accent est principalement mis sur le fait que certaines différences observées ne sont pas significatives sur plan statistique, cela ayant pour conséquence que des pays obtenant des scores et des rangs différents à la seule lecture des chiffres, réalisent pourtant des performances qui sont considérées comme équivalentes.

Si ce phénomène est bien admis quand les écarts de scores sont très faibles, soit de l’ordre de quelques points, ce n’est pas forcément le cas lorsqu’ils sont plus marqués. A titre d’illustration, pour la première enquête PISA réalisée en 2000 (OCDE, 2001) et en ce qui concerne la lecture, la France et le Japon n’affichaient pas des résultats différents sur le plan statistique alors que l’écart entre leurs scores respectifs était de 17 points (505 pour la France et 522 pour le Japon). En revanche, la performance de la Suède (score de 516) était estimée supérieure à celle de la France alors que l’écart entre les deux pays était seulement de 11 points. Un exemple encore plus caractéristique concernant les mêmes données est celui de la comparaison entre les Etats-Unis (score de 504) et la Pologne (score de 479), l’écart de 25 points n’étant pas significatif, les performances des deux pays pouvant alors être considérées comme comparables. Le graphique suivant permet de visualiser les écarts entre les pays cités, ceux qui sont reliés par un trait affichent des scores semblables sur le plan statistique alors que l’absence de trait entre les pays témoigne d’une différence significative.

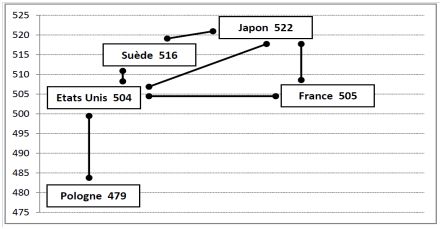
Graphique 1 : Comparaison des écarts de scores entre quelques pays à PISA 2000 en lecture

Cette question de la significativité des différences est toujours centrale en statistiques inférentielles et tient au fait que les données concernent des échantillons d’individus et non pas des populations entières. L’ampleur des écarts constatés, la taille des échantillons considérés, la dispersion des valeurs observées en leur sein et le degré de confiance souhaité dans les estimations sont autant d’éléments qui vont influer sur la précision des calculs, notamment pour l’estimation des scores moyens des élèves. De manière schématique (car d’autres paramètres interviennent également), on peut dire que les différences de performances entre pays auront toutes les chances d’être considérées comme significatives si i) les écarts observés sont importants, ii) les échantillons d’élèves sont de grande taille et iii) les écarts de scores entre les élèves d’un même pays sont réduits.

Lors du PISA 2009 se sont 470 000 élèves qui ont été testés dans 65 pays ; la taille des échantillons nationaux pour les pays de l’OCDE variait de 4410 élèves pour l’Islande à 38 210 élèves pour le Mexique (OCDE, 2011a). Malgré ces grands nombres, il existe pourtant toujours une incertitude liée aux erreurs d’échantillonnage et on doit interpréter les scores moyens en fonction d’un intervalle de confiance. La moyenne d’un pays est alors considérée comme une approximation plausible qui oscille entre des limites plus ou moins larges selon les pays et en fonction d’un certain seuil d’erreur[5]. Cet aspect statistique essentiel n’est pourtant pas forcément mis en avant dans les commentaires établis sur la base des résultats, car ce qui prime souvent pour les médias généralistes et pour les acteurs du monde politique, à différents échelons, c’est en premier lieu la place dans le classement et, en second lieu, les différences de points entre les pays pour établir des comparaisons géographiques ou temporelles. Mais, au-delà de cet aspect classique en statistiques, l’interprétation des scores pose aussi la question de l’échelle de mesure choisie par les concepteurs du programme PISA pour chiffrer le niveau de compétences des élèves. C’est particulièrement ce point que nous allons examiner dans ce texte avec pour objectif de proposer une autre lecture des résultats de PISA, plus adaptée aux acteurs (décideurs, enseignants et acteurs du secteur éducatif au sens large) afin qu’ils puissent mieux prendre conscience des risques d’une interprétation erronée des scores produits sur la base de l’échelle de mesure initiale et, d’une certaine manière, relativiser la lecture du classement international établi en fonction des résultats moyens des élèves.

L’enquête PISA, comme d’autres enquêtes internationales (PIRLS[6] notamment) fixe la moyenne des scores des élèves à 500 avec un écart-type de 100[7], cette échelle arbitraire présentant un avantage majeur qui est celui la distinguer, d’une part d’autres échelles utilisées dans d’autres tests très connus[8] et, d’autre part, des barèmes de notation traditionnels des élèves en vigueur dans les systèmes scolaires. En outre, la distribution des scores des élèves suit la loi normale[9] dont la connaissance des propriétés statistiques est essentielle pour comprendre la manière dont ces scores se répartissent autour de la moyenne (graphique 2). Sans développer ici les propriétés de la loi normale, on signalera seulement que la courbe dérivée de cette loi a une allure bien connue en forme de cloche qui met en évidence la concentration des valeurs autour de la moyenne ce qui a pour conséquence que plus les valeurs s’éloignent de cette moyenne, plus leur fréquence d’apparition devient faible. Ainsi, environ les deux-tiers des valeurs sont comprises entre plus ou moins un écart-type autour de la moyenne, 95% des valeurs sont comprises entre la moyenne et plus ou moins deux écart-types et presque la totalité des valeurs entre la moyenne et plus ou moins trois écart-types. Concrètement, dans l’échelle de PISA, les deux-tiers des élèves ont donc un score compris entre 400 et 600 points (puisque l’écart-type est de 100), 95% entre 300 et 700 point et 99% entre 200 et 800 points.

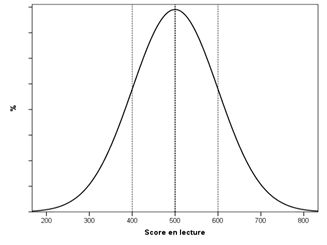
Graphique 2 : Distribution statistique des scores à PISA

Ce constat nous invite de suite à relativiser les différences de scores moyens entre pays, puisque beaucoup d’entre eux sont en fait peu éloignés de la moyenne internationale. Pour l’enquête PISA de 2009, les scores de lecture sur l’ensemble des pays participants à l’enquête variaient de 556 pour Shanghai à 314 pour le Kyrgyzstan. La variation est nettement plus faible si l’on ne considère que les pays de l’OCDE dans la comparaison. En effet, le pays à la tête du classement est la Corée avec 539 points et c’est le Mexique qui affiche le score le plus faible avec 425 points. Sur les 34 pays de l’OCDE qui ont participé à PISA 2009, 22 d’entre eux (soir 65%) ont un score compris entre 480 et 520 points et quinze (soit 44%) obtiennent un score compris entre 490 et 510 (graphique 3). Les écarts entre pays sont donc globalement faibles et, sur le plan statistique, l’appartenance à un pays n’explique que dix pour-cent des différences (de la variance) de scores entre les élèves (OCDE, 2004).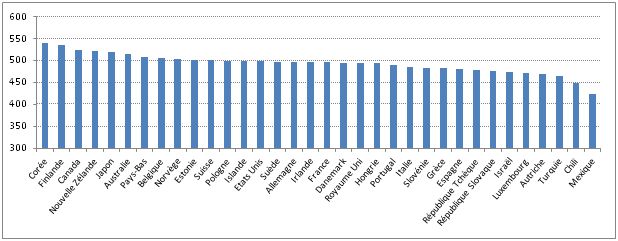

Graphique 3 : Scores moyens des pays de l’OCDE à PISA 2009 en lecture

Autrement dit, les écarts entre pays sont minimes par rapport aux différences de scores entre les élèves d’un même pays. Même si au niveau visuel, et sur la base des représentations graphiques qui accompagnent les commentaires dans les rapports, on constate bien la faible variation des scores entre de nombreux pays, il reste que l’échelle de mesure de PISA, exprimée en centaines de points, n’est pas familière au public et peut, d’une certaine manière, donner une image plus accentuée de la situation réelle. Ainsi, ce sont davantage les écarts absolus exprimés en points qui sont commentés au détriment des écarts relatifs (en unités d’écart-type) pourtant plus pertinents pour les chercheurs. L’idée est donc ici de proposer une lecture plus directe des résultats de l’enquête PISA afin de relativiser le classement international et de mettre davantage en évidence ce qui est le plus significatif dans les résultats obtenus, à savoir les différences entre les élèves.

Pour tendre vers cet objectif, nous avons choisi d’exprimer les scores obtenus à PISA dans une échelle connue et partagée par l’ensemble de la population, à savoir celle utilisée par le système de notation scolaire. Sur le plan scientifique, ce choix peut à juste titre être considéré comme peu académique, voire même incongru au niveau de la méthode puisque la notion de score mobilisée dans PISA diffère fondamentalement de la notion de note. On ne rappellera pas ici les biais individuels et contextuels associés à la notation scolaire qui produisent notamment des inégalités et des injustices de traitement entre les élèves (Merle, 1998) ; en fait, l’idée est davantage de s’appuyer sur deux caractéristiques de la note scolaire qui nous semblent importants dans notre démarche.

La première caractéristique, centrale pour notre raisonnement, est liée au caractère connu du système de notation au sein des pays qui le pratique. En effet, chaque citoyen, en tant qu’élève tout d’abord, a lui-même été soumis à cette pratique au cours de sa scolarité et, pour beaucoup, cette familiarité est entretenue ensuite par le suivi du parcours scolaire de la génération qui lui succède. L’échelle de notation est donc de suite interprétable, tant au niveau de la moyenne que des variations des valeurs autour de celle-ci. La seconde caractéristique concerne une propriété statistique de l’échelle de notation. Dans beaucoup de contextes (les pays, les niveaux de la scolarité…) les enseignants tendent à répartir les notes au sein de leur classe selon une courbe gaussienne avec une concentration autour de la moyenne et peu de notes très faibles ou très hautes en référence au barème. Cette pratique illustre bien l’évaluation normative pratiquée dans les systèmes d’enseignement qui consiste, quel que soit le niveau réel des élèves de la classe, à adopter ce type de répartition. Il est connu depuis longtemps sous le nom d’effet Posthumus[10] (Crahay, 2003). Cette seconde caractéristique de la notation nous est particulièrement utile puisque les scores estimés par PISA se répartissent de la même manière.

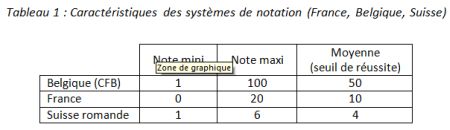
De nombreux systèmes de notation des élèves existent à travers le monde avec des modalités très variables (OCDE, 2013). Certains pays utilisent des fourchettes réduites de 1 à 5 points (Portugal, Autriche, Hongrie) alors que d’autres évaluent les élèves avec une amplitude allant de 1 à 100 (Irlande, Singapour, Belgique). Les notes minimales requises (pour la promotion dans le niveau supérieur) diffèrent aussi entre les pays et ne correspondent pas toujours au milieu de l’échelle de notation. Afin de conduire notre démonstration sur la base de plusieurs barèmes de notation volontairement variés, et pour mieux percevoir la relativité du classement international, nous avons considéré trois contextes nationaux : Belgique, France et Suisse. L’exercice consistera donc à exprimer les scores de PISA en fonction des trois échelles de notation présents dans ces contextes. Dans un premier temps, nous présenterons les résultats globaux entre les pays puis, dans un second temps, nous nous intéresserons aux différences de scores entre les élèves au sein des pays. C’est donc bien une lecture renouvelée des résultats à PISA que nous proposons, plus lisible pour le public et pouvant permettre des interprétations plus adéquates de certaines conclusions tirées de l’enquête internationale. Dans les trois exemples retenus, les systèmes de notation des élèves dans l’enseignement secondaire sont totalement différents puisque la France utilise un barème avec des notes pouvant, dans l’absolu, varier de 0 à 20, la moyenne (seuil de suffisance) étant fixée à 10. En Communauté française de Belgique les notes peuvent varier de 1 à 100, le seuil de réussite étant de 50. Pour la Suisse, l’échelle de notation varie de 1 à 6 avec un seuil de suffisance fixé à 4 points (tableau 1).

Il s’agit donc concrètement d’exprimer les scores des différents pays de l’OCDE à PISA 2009 en lecture sur la base de ces nouvelles échelles, sachant que sur l’ensemble de l’échantillon la moyenne est 493 et l’écart-type de 93. Nous émettons donc l’hypothèse probable selon laquelle les notes des élèves dans les trois pays ou régions considérés suivent une répartition proche d’une distribution gaussienne, comme c’est le cas pour PISA. En appliquant le même rapport de l’écart-type sur la moyenne (autrement dit le coefficient de variation) que celui de PISA, en l’occurrence 0,19 (soit 93 / 493), les écart-types des nouvelles distributions de notes prennent alors les valeurs suivantes : 9,5 pour le système de notation Belge, 1,9 pour le système Français et 0,76 pour le barème Suisse. Il est ensuite possible, sur la base de ces nouveaux paramètres, de calculer une note pour chacun des pays. Le tableau 2 présente ces données dans les trois échelles retenues et fait figurer également le score à PISA dans l’échelle d’origine, son écart-type et le coefficient de variation (tableau 2). On peut donc situer chaque pays avec une nouvelle référence par rapport à la moyenne des pays de l’OCDE.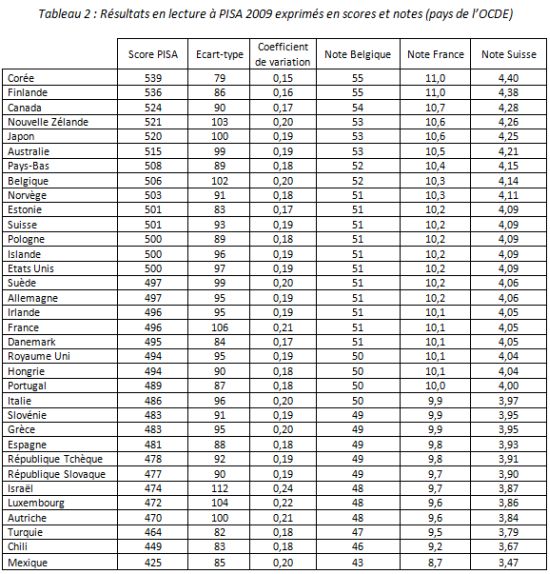

Les trois graphiques qui suivent permettent de mieux visualiser les résultats de PISA exprimés dans chacune des trois échelles de notation.

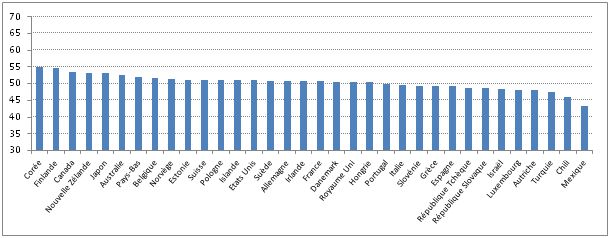
Graphique 4 : Scores moyens des pays de l’OCDE à PISA 2009 en lecture

exprimés dans l’échelle de notation belge

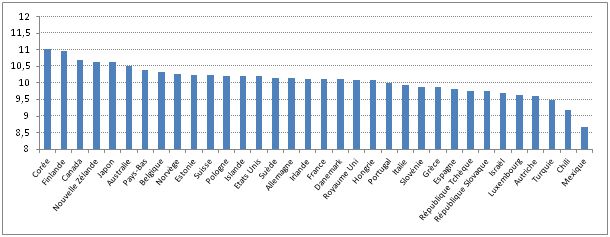
Graphique 5 : Scores moyens des pays de l’OCDE à PISA 2009 en lecture

exprimés dans l’échelle de notation française

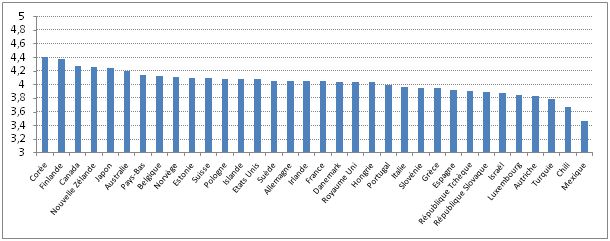
Graphique 6 : Scores moyens des pays de l’OCDE à PISA 2009 en lecture

exprimés dans l’échelle de notation suisse

L’impression qui se dégage de la lecture du tableau et des graphiques est bien le caractère relatif des différences de performances entre les pays. Ainsi, en raisonnant dans la logique du système de notation français, la Corée qui arrive en tête du classement de l’OCDE affiche une note de 11 sur 20 et le Mexique, situé à la dernière place, obtient une note de 8,7, soit un écart de 2,3 points. Les valeurs pour ces deux pays avec le système belge sont de 55 et de 43 et de 4,4 et 3,5 avec le système de notation suisse (graphique 7).

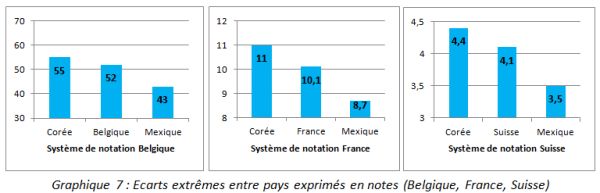
Graphique 7 : Ecarts extrêmes entre pays exprimés en notes (Belgique, France, Suisse)

Le constat de proximité des notes est donc évidemment plus marqué si l’on fait porter la comparaison sur des pays aux performances plus voisines. Ainsi, la Finlande (score de 536 à PISA), très souvent citée en exemple pour la qualité de son système éducatif est, comme la Corée, distante de la France (score de 496) de seulement 0,9 points si l’on raisonne en note (11 pour la Finlande et 10,1 pour la France). L’interprétation des écarts entre pays apparaît donc bien différente de celle basée sur le seul classement pour lequel, de fait, les écarts entre les places sont perçus constants. On voit bien ainsi que de dire par exemple que la France est classée au 18^ème rang sur les 34 pays de l’OCDE n’invite pas aux mêmes commentaires que de dire que le premier pays du classement ne dépasse la France que de 0,9 points sur une échelle de 0 à 20. Les notes permettent donc pour le grand public, plus que les scores d’origine, de mieux percevoir et de relativiser les différences entre les pays.

C’est donc surtout la variabilité des performances entre les élèves qui apparaît importante dans une telle enquête. Pour en avoir une représentation plus concrète, nous avons également simulé, toujours sur la base des échelles de notation, la dispersion des scores des élèves au sein d’un même pays, celle-ci étant variable au regard des valeurs des coefficients de variation (tableau 2). Certains pays affichent une forte dispersion des résultats des élèves, comme Israël et le Luxembourg, d’autres au contraire ont des performances plus homogènes, c’est le cas de la Corée et de la Finlande qui sont, par ailleurs, les pays à la tête de classement. Sur la base du système de notation français, on constate qu’en Corée les notes des deux-tiers des élèves sont comprises entre 9,4 et 12,6 alors que pour le Luxembourg, la même proportion d’élèves a une note comprise entre 7,5 et 11,8, soit une hétérogénéité beaucoup plus marquée. Les notes pour la Corée, et toujours pour les deux-tiers des élèves, varient entre 47 et 63 dans le système belge et de 3,8 à 5 dans le système suisse. Pour le Luxembourg la fourchette s’étale de 38 à 59 dans l’échelle de notation belge et de 3 à 4,7 pour la Suisse. Ces différences de scores entre les élèves invitent donc d’autant plus à relativiser les écarts entre pays exposées précédemment. Les graphiques suivants permettent de comparer, dans chacun des systèmes de notation retenus, les écarts moyens entre les pays de l’OCDE avec les écarts moyens entre les élèves, la notion d’écart moyen correspondant ici aux écart-types des distributions des scores entre pays et entre élèves. Dans l’échelle de notation française, l’écart moyen entre les élèves est de 1,9 points alors que l’écart moyen entre les pays est seulement de 0,47 points ; les chiffres dans l’échelle de notation belge sont de 9,5 (entre élèves) et de 2,3 (entre pays) et pour le système suisse de 0,76 (entre élèves) et 0,19 (entre pays).

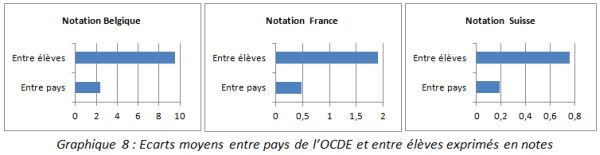
Graphique 8 : Ecarts moyens entre pays de l’OCDE et entre élèves exprimés en notes

On peut aussi illustrer cette dispersion entre les résultats des élèves en considérant les différents niveaux de compétences à PISA. On rappellera à ce titre que les performances des élèves peuvent être hiérarchisées en plusieurs niveaux (tableau 3). Pour la lecture en 2009, sept niveaux sont définis : 1b, 1a, 2, 3, 4, 5 et 6. Chacun de ces niveaux correspond, à la fois à un certain degré de maîtrise des compétences et à un certain niveau de score dans l’échelle de PISA. Ainsi, pour être considérés comme bons lecteurs, les élèves de 15 ans doivent atteindre au moins le niveau 5, soit un score supérieur à 625. A ce niveau, les élèves sont capables de retrouver des informations qui sont profondément enfouies dans le texte et d’en inférer les informations pertinentes, ils sont aussi capables de comprendre des concepts inattendus (OCDE, 2011a).

Tableau 3 : Niveaux de compétence en compréhension de l’écrit à PISA 2009

Source : OCDE, 2010

Ce score minimal de 625 correspond dans les échelles retenues, aux notes de 12,7 (France), 64 (Belgique) et 5,1 (Suisse). Si l’on considère à présent le niveau de compétence le plus bas (soit le niveau 1b), les scores correspondants sont compris entre 262 et 334 points. Cet intervalle se traduit par des notes comprises entre 5,4 et 6,8 (France), 27 et 34 (Belgique), 2,1 et 2,7 (Suisse). Tous ces chiffres qui témoignent du degré de maîtrise des compétences variable montrent bien aussi que l’amplitude des performances entre les élèves dépasse de loin, celle des résultats entre les pays. Le graphique suivent présente dans l’échelle de notation française les différents niveaux de compétence définis par PISA.

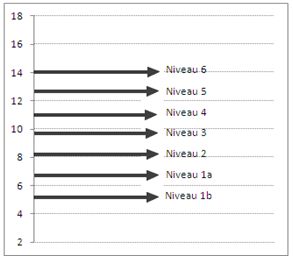
Graphique 9 : Niveaux de compétence en lecture à PISA 20009 (échelle de notation française)

Compte tenu de la répartition gaussienne des scores, peu d’élèves affichent des performances qui correspondent aux niveaux extrêmes, mais il existe de fortes différences entre pays dans cette répartition par niveaux. Au niveau de l’OCDE, on relève en 2009 5,7% d’élèves très faibles (niveau 1b et inférieur à 1b) alors que cette proportion est de 7,9% pour la France (pour mémoire, cette proportion n’était que de 6% en 2000). Il est aussi possible de présenter la répartition des élèves selon les différents niveaux sur la base des notes. Le graphique suivant présente cette répartition pour la France avec son système de notation. Les écarts de notes entre élèves permettent de rendre compte de manière directe des écarts de compétences en compréhension de l’écrit.

Graphique 10 : Répartition des élèves français selon les niveaux de compétence en lecture à PISA 20009 avec l’échelle de notation Française

On pourrait bien sûr mobiliser d’autres critères pour insister sur les différences inter-individuelles au sein des pays. Par exemple, entre les filles et les garçons ou encore selon le milieu socio-économique (OCDE,2011b). A titre d’illustration, sur l’échantillon des pays de l’OCDE en 2009, le score moyen des filles est de 513 et celui des garçons de 474, ce qui se traduit par des notes de 10,5 (filles) et 9,7 (garçons) dans le système français. Les écarts liés à l’influence du milieu social sont nettement plus marqués. Pour l’ensemble des pays de l’OCDE, l’augmentation d’une unité de l’indice PISA de statut économique social et culturel entraîne une augmentation de score 38 points, soit 0,8 points si on l’exprime en notes (système français). Pour la France cet impact du milieu social est de 51 points dans l’échelle de PISA, soit 1 point dans l’échelle de notation français (de 0 à 20), ce qui est du même ordre que l’écart de performances moyennes entre le Portugal (22^ème dans le classement) et la Finlande (2^ème du classement).

Pour conclure

En conclusion, on rappellera que l’objectif de ce texte était de proposer une autre lecture des résultats de l’enquête PISA, certes pas très conventionnelle sur le plan scientifique, mais qui peut permettre de mieux interpréter les classements produits par cette enquête internationale. En effet, malgré les précautions prises dans les diverses publications de l’OCDE et celles des responsables des consortiums PISA, les écarts de scores entre les pays sont très souvent surestimés dans les commentaires réalisés par les médias et les conclusions qui en découlent peuvent être erronées (Grenet, 2008). Le fait de raisonner en termes de notes pour les besoins de l’exercice plutôt qu’en score permet de relativiser la notion de classement entre les pays ainsi que les écarts entre les scores moyens, c’est particulièrement le cas pour les pays comparables sur le plan du développement économique. Notre démarche ne remet nullement en cause l’intérêt du programme PISA pour les politiques éducatives mais permet de mettre surtout l’accent sur les différences de performances entre les élèves plutôt que sur les écarts entre pays. Cela permet aussi de souligner que la vraie marge d’action se situe au sein de chaque contexte national pour notamment réduire les écarts entre les élèves et permettre au plus grand nombre d’entre eux, et quelles que soient leurs caractéristiques, d’atteindre un niveau de compétences suffisant pour la suite de leur scolarité et, plus largement, pour leur insertion sociale et professionnelle.

Bruno Suchaut

URSP (Unité de recherche pour le pilotage des systèmes pédagogiques)

Références

Antibi A. (2003), La constante macabre ou comment a-t-on découragé des générations d’élèves ? Paris, Nathan.

Bautier E., Crinon J., Rayou P., Rochex J.Y. (2006). Performances en littératie, mode de faire et univers mobilisés par les élèves ; analyses secondaires de l’enquête PISA 2000 ». Revue française de pédagogie, n° 157, p.85-101.

Bottani N., Vrignaud P. (2005). La France et les évaluations internationales. Paris : Ministère de l’Éducation nationale.

Crahay M. (2003), Peut-on lutter contre l’échec scolaire? de Boeck, 2003

Duru-Bellat M., Mons N., Suchaut B. (2004), Organisation scolaire et inégalités sociales de performances : les enseignements de l’enquête PISA. Éducation et formations, n° 70, p.123-131.

Grenet J. (2008), PISA : une enquête bancale ? La vie des idées.

Merle P. (1998), Sociologie de l’évaluation scolaire, Paris, PUF, 1998.

Mons N. (2008), Evaluation des politiques éducatives et comparaisons internationales : introduction. Revue française de pédagogie, n° 164, p.5-13.

OCDE (2001), Connaissances et compétences : des atouts pour la vie, premiers résultats de PISA 2000.

OCDE (2004). Apprendre aujourd’hui pour réussir demain. Premiers résultats de PISA 2003.

OCDE (2010). Résultats du PISA 2009 : Synthèse. OCDE, 2010.

OCDE (2011a). Résultats du PISA 2009 : Savoirs et savoir-faire des élèves Performance des élèves en compréhension de l’écrit, en mathématiques et en sciences (Vol. I)

OCDE (2011b), Résultats du PISA 2009 : Surmonter le milieu social : L’égalité des chances et l’équité du rendement de l’apprentissage. (Volume II), PISA, Éditions OCDE.

OCDE (2013), Les grandes espérances : comment les notes et les politiques éducatives façonnent-elles les aspirations des élèves ? Pisa in Focus, n° 26, février 2013, 4 p.

Olsen R.V., Lie S. (2006), Les évaluations internationales et la recherche en éducation : principaux

objectifs et perspectives. Revue française de pédagogie, n° 157, p.11-26.

Rey O. (2011), PISA : ce que l’on en sait et ce que l’on en fait». Dossier d’actualité Veille et Analyses, n°66, octobre 2011.

Robin I. (2002), L’enquête PISA sur les compétences en lecture des élèves de 15 ans : trois biais culturels en question. VEI Enjeux, n° 129, juin 2002 pp. 65 91.

Vrignaud P.(2006). La mesure de la littératie dans PISA : la méthodologie est la réponse, mais quelle était la question ? Revue française de pédagogie, n° 157, p.27-41.