Parmi toutes les épreuves de mathématiques, on s’attachera à analyser celle qui a stupéfié la plupart des professeurs des écoles : elle est décrite comme permettant de tester l’usage d’un nombre comme moyen de repérer une position. Pour la quasi totalité des professeurs, il était inimaginable que l’on puisse proposer une telle tâche à l’entrée au CP. Alors d’où vient cette idée ? Nous verrons qu’elle est issue des travaux de Stanislas Dehaene (SD), un chercheur en psychologie cognitive dont les thèses, dans ce domaine, sont extrêmement controversées. Le ministre vante le caractère scientifique de ces évaluations alors que c’est un point de vue opposé à celui SD qui, aujourd’hui, tend à devenir prépondérant. L’enjeu n’est pas mince : suivre SD sur cette question, ce serait revenir aux pratiques pédagogiques responsables de l’effondrement du calcul en France.

Comment l’épreuve est présentée aux enseignants

Dans l’un des items, l’enfant est face à un segment dont chaque extrémité est numérotée, avec par exemple 0 et 10, on lui indique une position et, parmi plusieurs propositions d’écritures chiffrées, il doit choisir celle qui correspond à cette position.

On peut tout d’abord remarquer que la réponse correcte ne s’impose pas d’emblée comme une évidence, même lorsqu’on a une bonne culture mathématique (3 n’est pas proposé comme réponse possible, mais ne serait-ce pas un oubli ?). C’est seulement en mesurant et en se livrant à un petit calcul de proportionnalité que la certitude s’établit : la réponse est 4. Continuons à analyser cette tâche de manière ordinaire, sans faire appel à une théorie en neurosciences cognitives. Dans une vidéo mise en ligne sur le site Eduscol, Michel Fayol explique aux professeurs des écoles et aux parents l’intérêt de cette épreuve : « (Elle) permet d’avoir une très bonne indication sur la capacité à mettre en relation un symbole, le chiffre arabe, et la quantité correspondante ».

Ces propos sont très surprenants : de quelles quantités parle Michel Fayol ? Quelles quantités un enfant qui entre au CP est-il susceptible d’imaginer à partir d’un tel dessin ? Il voit bien l’écriture chiffrée « 10 », mais où sont les 10 unités correspondantes ? Et pourquoi écrit-on « 0 » au-dessus d’un trait alors que 0 est censé correspondre à l’absence de toute unité ? Ce mode de représentation est a priori totalement incompréhensible pour un enfant sortant d’école maternelle.

En 1987, Gérard Vergnaud a rédigé un chapitre d’un ouvrage de la Pléiade coordonné par Jean Piaget dans lequel il se livre à une analyse de l’« appropriation d’un signifiant complexe : la droite numérique » et il donne les clés permettant de comprendre la difficulté de la tâche proposée. Sur une ligne numérique, les unités existent mais la façon dont les chiffres en désignent les quantités est particulièrement obscure. Ainsi, dans le haut du schéma ci-dessous on comprend facilement le rapport entre unités et chiffres, alors que sur la ligne numérique du bas il devient moins clair.

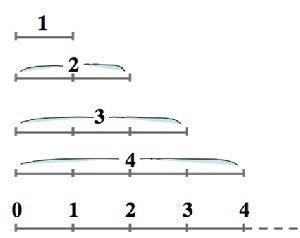
Deux opérations de pensée sont nécessaires pour passer des quatre représentations du haut à la ligne numérique du bas tout en continuant à donner du sens à cette représentation : 1°) Il faut comprendre que les chiffres ont été déportés vers l’extrémité de droite plutôt que de rester centrés sur la quantité qu’ils représentent (Gérard Vergnaud appelle cela la « ponctualisation de la désignation des quantités ») et 2°) Il faut « fusionner » les différentes représentations du haut de façon à inclure les différentes quantités l’une dans l’autre (« inclusion des quantités »).

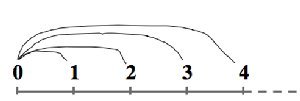
Gérard Vergnaud montre que l’usage d’une ligne numérique pour représenter des quantités telles que des durées reste difficile en cycle 3. Karen Fuson, très grande chercheuse en psychologie des apprentissages numériques qui est proche de l’école parce qu’elle est l’auteure d’une méthode d’apprentissage, en souligne elle aussi la complexité dans de nombreux articles. Comment les enfants apprennent-ils cet outil de représentation ? Très vraisemblablement en apprenant comment le double-décimètre permet de mesurer des longueurs. Les deux opérations de pensée qui viennent d’être explicitées sont en effet la clé d’un usage réfléchi de cet outil.

Les auteurs de l’évaluation d’entrée au CP et au CE1 savent-il que l’apprentissage de la mesure des longueurs commence seulement au CP et ne se consolide vraiment qu’au CE1 ? Savent-ils que lorsque 0 n’est plus la borne de gauche, comme c’est le cas dans l’épreuve de début CE1, la difficulté est démultipliée ?

Une déconnexion entre les résultats et les compétences arithmétiques réelles

Ayant regardé les résultats d’une classe de CE1, il sautait aux yeux que chez 9 élèves sur 28 les résultats à cette épreuve étaient totalement déconnectés de leurs compétences arithmétiques réelles. Ainsi, l’un des élèves a 93% de réussite en moyenne aux autres épreuves numériques (l’épreuve de rapidité a été exclue) mais il n’a que 33% de réussite au placement d’un nombre sur un segment numéroté à ses extrémités. Et pourtant il a 100% de réussite à la résolution de problèmes arithmétiques dont certains sont loin d’être faciles ! Qui peut penser qu’un tel enfant n’aurait pas la « capacité à mettre en relation un symbole, le chiffre arabe, et la quantité correspondante ». Michel Fayol peut-il réellement soutenir que l’épreuve controversée est un bon indicateur de cette capacité ?

Alors d’où vient cette idée folle de proposer une telle tâche dès l’entrée du CP ? Elle provient des travaux de Stanislas Dehaene, le récent président du Conseil Scientifique de l’Éducation Nationale.

Un résumé des thèses de Stanislas Dehaene

Pour lui, le bébé naitrait avec un « système approximatif des nombres » ou encore avec un « sens approximatif des nombres ». Il parle également d’une « ligne mentale approximative des nombres ». Cette compétence, soi-disant innée, explique le titre provocateur de son principal ouvrage sur le sujet : « La bosse des maths » (en anglais, le titre est : « The number sense »).

Chez le bébé, chez l’enfant et chez les peuples sans arithmétique, la ligne numérique mentale ne serait pas structurée comme chez l’adulte cultivé : les premiers nombres apparaitraient plus distincts, ils seraient plus espacés que les suivants et, de manière générale, seraient de moins en moins espacés au fur et à mesure qu’ils grandissent. Chez l’enfant, cette ligne numérique subjective ressemblerait donc à ceci, par exemple : 

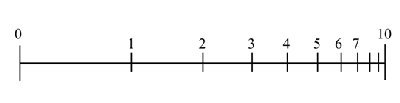
On comprend mieux l’origine du test des évaluations CP (et CE1) : si l’on pointe un point un peu à gauche du milieu d’un segment numéroté entre 0 et 10, l’enfant va-t-il dire qu’il correspond à 4 (bonne réponse), ou à 3 voire 2, réponses qui sont censées révéler une échelle subjective immature, celle des bébés ou des indiens Mundurukus.

Comment SD conçoit-il le progrès depuis une échelle subjective immature vers une échelle subjective telle que l’écart entre 0 et 1, celui entre 1 et 2, entre 2 et 3, entre 3 et 4… est constant ? Pour lui, ce progrès résulte de l’apprentissage du comptage-numérotage. Or, tous les enseignants savent ce qui se passe chez les élèves à qui l’on enseigne le comptage-numérotage. Pour représenter une quantité, l’enfant apprend à pointer successivement les unités tout en prononçant : 1231567, par exemple. Progressivement, il apprend que si une collection de pots de peinture est comptée 1231567 et une collection de pinceaux est également comptée 1231567, alors on peut mettre exactement 1 pinceau par pot : il y a la même quantité de pinceaux que de pots (la suite des mots 1234567 fonctionne comme collection intermédiaire). Il apprend de plus qu’il suffit de mémoriser le dernier mot prononcé, 7, pour savoir jusqu’où il faut compter, il se met à dire : 1234567, 7. Dans cette procédure, le premier « 7 » est une sorte de numéro que l’enfant prononce alors qu’il pointe la 7ième unité. En revanche, la seconde occurrence de « 7 » désigne la quantité totale.

Tout cela se comprend aisément, mais comment l’enfant apprend-t-il que l’écart entre 0 et 1, celui entre 1 et 2, entre 2 et 3, entre 3 et 4… est constant et égal à 1 ? SD considère que c’est un mystère. En 2012, lors d’un conférence nationale consacrée à l’enseignement des mathématiques, il parle ainsi de l’accès à un écart constant entre les nombres : « C’est un grand changement mental. Mais on ne comprend pas très bien ce qui se passe ; il y a une sorte de révolution mentale et un changement théorique très abstrait qui se produit. Si on identifiait proprement chacune de ces transitions, on saurait que là, il faut faire très attention parce qu’il y a quelque chose de crucial qui doit changer. »

Or, d’une part toutes ces thèses de SD : compétences innées, représentation mentale des nombres, rôle du comptage-numérotage, sont extrêmement controversées et, d’autre part, les pédagogues en connaissent plus sur les clés du progrès que SD. Montrons-le.

Il faut parler d’ « ordre de grandeur » et non de « nombres approximatifs »

Tous les chercheurs sont d’accord pour considérer que les bébés naissent avec un système leur permettant de distinguer deux durées, deux longueurs, deux collections… lorsqu’elles diffèrent suffisamment. Alors que SD parle de « système de nombres approximatifs », de nombreux chercheurs préfèrent, de manière plus neutre, parler de « système de grandeurs approximatives » (traduction de « approximative magnitude system »). Le mot anglais « magnitude » qui se traduit par « ordre de grandeur » est celui qui permet le mieux d’exprimer ce que sont les compétences réelles des bébés. Pour le dire rapidement, l’adaptation a bien fait son travail : tous les animaux, précocement, savent distinguer un gros tas de nourriture d’un petit tas de nourriture.

Présentons un résultat qui invite à se méfier de l’idée que les bébés disposeraient de « nombres approximatifs » ou même de « quantités approximatives » : les nourrissons de moins de trois jours différencient une collection de 10 et une autre de 30, par exemple, c’est-à-dire de grandes collections qui sont dans un rapport de 1 à 3.  En revanche, des bébés bien plus âgés ne font pas la différence entre une collection de 2 et une de 6, c’est-à-dire de petites collections qui, elles aussi, sont dans un rapport de 1 à 3. C’est totalement contre intuitif : les bébés réussissent avec de grandes collections ce qu’ils échouent avec de petites collections ! Ceci plaide en faveur de l’hypothèse que le traitement inné des collections ne porte ni sur des quantités, ni sur des nombres, mais sur des ordres de grandeur. En effet, avec les petites collections le bébé prend vraisemblablement en compte les différentes unités des collections. Et il échoue ! En revanche, avec de grandes collections, leur taille l’empêche de prendre en compte les différentes unités, l’obligeant à traiter les collections plus globalement. Et il réussit. Or, on ne peut pas parler de quantités ou de nombres sans qu’il y ait une prise en compte des différentes unités (SD lui-même l’admet). Les bébés échouant quand ils traitent les différentes unités, on peut en conclure que leurs connaissances innées sont relatives à des ordres de grandeurs (magnitudes), pas à des quantités et encore moins à des nombres. Même lorsqu’on parle de « quantités ou de nombres approximatifs », l’usage des mots « quantité » et « nombre » est inapproprié.

Il n’y a pas de « droite mentale innée » dont les écarts deviendraient réguliers

Pourquoi, chez le bébé et chez l’enfant, la représentation des ordres de grandeurs serait-elle organisée selon une « ligne droite mentale » ? Comparons avec le cas des couleurs : on a montré qu’à 4 mois les bébés distinguent les couleurs dès que celles-ci sont suffisamment différentes. Et pourtant, personne n’a envie de dire qu’ils possèdent un cercle chromatique mental approximatif ! Projeter chez le bébé et chez l’enfant une organisation spatiale, ligne droite dans le cas des ordres de grandeur, cercle dans celui des couleurs, alors que cette organisation est celle d’une personne savante, est extrêmement spéculatif.

On a vu que selon SD, l’apprentissage du comptage conduirait à un changement dans la façon dont les points correspondants aux différentes quantités se répartissent sur la « ligne droite mentale » des très jeunes enfants. Initialement, plus les quantités sont petites, plus elles apparaissent distinctes et, donc, plus les points sont espacés. Et, sur cette échelle, avec le progrès, les écarts deviendraient progressivement réguliers, comme sur une règle graduée. Pour SD, c’est la représentation innée elle-même qui se restructurerait progressivement.

Lors d’un colloque qu’il a organisé au Collège de France, l’un des grands neuropsychologues contemporain, Brian Butterworth, s’inscrit en faux contre cette théorie : l’intuition innée resterait ce qu’elle était. Lorsqu’on demande à une personne arithmétisée de placer divers points sur une droite, c’est au moment de placer les points sur une ligne que celle-ci utiliserait ses connaissances numériques pour régulariser les écarts. Il conclut même son exposé en disant qu’un célèbre effet expérimental mis en évidence par SD et qui est en jeu dans cette affaire, est peut-être un « Boojum » (créature imaginaire dans « La Chasse au Snark » de Lewis Carrol).

Le rôle central de la représentation innée des ordres de grandeur mis en cause

La théorie (plutôt innéiste) selon laquelle les connaissances numériques se développeraient en s’appuyant sur le système approximatif des ordres de grandeur, est fortement mise en cause aujourd’hui. Longtemps controversée, cette théorie se trouve fortement ébranlée par une recherche qui vient d’être publiée (Lyons et collègues, 2018). Ces chercheurs montrent que, chez des enfants de 5 ans, les progrès du système approximatif résultent des progrès de leur connaissances numériques alors que, en revanche, rien n’indique que les progrès dans leurs connaissances numériques dépendraient de ceux du système approximatif. En bref, ce serait pour l’essentiel l’apprentissage et l’enseignement des nombres qui importerait.

Une théorie alternative

Une des principales théoriciennes du domaine, Elisabeth Spelke, professeur de psychologie à Harvard et nouvelle membre du Conseil scientifique de l’Éducation nationale,  a écrit en 2017 dans un article de synthèse : « [I reject] the thesis that counting is central to number » ? Quand Elisabeth Spelke parle de « comptage », il faut évidemment comprendre qu’il s’agit du comptage-numérotage, celui que le sens commun pense être la seule forme de comptage qui puisse être enseignée. Pour Elisabeth Spelke, quelle serait la clé du progrès ? Le fait de parler les nombres pour les mettre en relation : « 5 crayons, c’est 3 crayons et encore 2 crayons », par exemple.

Or cette théorie est complètement compatible avec ce qu’était la pédagogie officielle du nombre dans l’école française entre 1945 et 1970. Henri Canac, l’un des grands pédagogues de l’époque, écrivait en 1955 que connaitre un nombre donné, c’est en maitriser « ses diverses décompositions en nombres moins élevés que lui ». On pourrait ajouter : c’est de plus savoir l’utiliser pour en former de plus grands. Et l’enseignement du comptage, que devenait-il dans une telle perspective ? René Brandicourt, un autre grand pédagogue de l’époque mettait en garde contre l’enseignement du comptage-numérotage (1962) ; à cet effet, il imaginait une personne qui dispose d’assiettes alignées devant lui et qui veut les dénombrer en les prenant une à une pour former une pile : « nous signalons le danger qu'il y a, dans le comptage, à énoncer les nombres en prenant les objets un à un. C'est en posant la 2e assiette sur la 1re que je dis 2, non en la prenant en mains (la 2e n'est pas 2, elle est 1) ; ibid. pour la 3e, la 4e... C'est en examinant la pile successivement constituée que j'énonce 2, 3 , 4... 6. »

La façon dont René Brandicourt recommande d’enseigner le comptage est très différente de celle préconisée par SD : le but est d’éliminer tout usage de numéros pour compter sous la forme « 1 plus 1, 2 ; plus 1, 3 ; plus 1, 4 ; plus 1… » Chacun des mots prononcés désigne une quantité (celle des assiettes de la pile successivement constituée) et le pédagogue peut même expliciter d’emblée le calcul « + 1 » répété sous-jacent au comptage. L’enfant rentre d’emblée dans le calcul, on lui enseigne d’emblée la propriété dont la plupart des chercheurs en psychologie cognitive considère aujourd’hui qu’elle fonde le nombre : l’itération de l’unité.

Dans un tel cadre théorique, comment les enfants découvrent-ils que l’écart entre 0 et 1, celui entre 1 et 2, entre 2 et 3, entre 3 et 4… est constant ? Ils l’apprennent d’emblée parce qu’on leur enseigne que cet écart est égal à 1. C’est ainsi qu’ils découvrent les nombres ! Le mystère sur lequel SD bute est donc levé.

Une théorie alternative confortée par les recherches dans de nombreux domaines

L’article d’Elisabeth Spelke montre que la théorie qu’elle avance est la plus raisonnable lorsque l’on prend en compte l’ensemble des résultats des recherches empiriques disponibles en psychologie et neuropsychologie cognitive. L’histoire des pratiques et des discours pédagogiques montre sans conteste que cette théorie est celle qui avait cours à une époque où les écoliers français calculaient encore bien.

En effet, la Depp (Rocher, 2008) a montré que les performances en calcul se sont effondrées durant la période 1987-1999, c’est-à-dire immédiatement après que le ministère ait recommandé d’enseigner le comptage-numérotage, à rebours de ce qui était préconisé auparavant. Toutes les autres enquêtes (PISA, TIMMS, Cèdre) ne font que confirmer que le niveau, depuis, ne s’est pas redressé. Les performances des écoliers français plafonnent au bas niveau de 1999. Après cette date, la dégradation n’est guère significative.

Psychologie cognitive, histoire des pratiques et des discours pédagogiques, enquêtes sociologiques, à cette liste de domaines de recherche, on pourrait ajouter la psychologie clinique des difficultés numériques : en effet, toutes les études montrent que les élèves en grande difficulté dans leurs apprentissages numériques sont des enfants enfermés dans des stratégies de comptage-numérotage. Ces stratégies de bas niveau qu’on leur a enseignées dans leur jeune âge se fossilisent. Henri Canac disait de ces enfants qu’ils avaient été « mal débutés ».

Psychologie cognitive, histoire des pratiques et des discours pédagogiques, enquêtes sociologiques, psychologie clinique des difficultés d’apprentissage : que vaut la théorie extrêmement spéculative de SD face à tant de points de vue convergents venus de tant de chercheurs différents dans des domaines différents ?

Vers un retour aux pratiques pédagogiques qui ont provoqué l’effondrement des performances en calcul ?

Les programmes 2015 ont effectué un véritable changement de cap, ils invitent à renouer avec la culture scolaire qui était la nôtre entre 1945 et 1970. C’est ainsi qu’on lit dans le programme maternelle que « les activités de dénombrement éviteront le comptage-numérotage ». Par ailleurs, les attendus de fin de maternelle fixent aujourd’hui comme objectif la maitrise des 10 premiers nombres seulement mais, évidemment, ils mettent l’accent sur celle de leurs décompositions et celle de la propriété « +1 répété » de la suite des nombres (itération de l’unité).

Or, que propose le ministère lorsque les élèves de CP échouent à apparier correctement les chiffres et les points d’un segment dont les extrémités sont repérées par 0 et 10 ? Pour que les élèves apprennent que l’écart entre deux nombres qui se suivent est constant et égal à 1, conforte-t-il les programmes 2015 en insistant sur la différence entre comptage-numérotage et comptage-dénombrement ? Insiste-t-il sur le rôle fondamental de l’itération de l’unité ?

Rien de tout cela. Sur le site Eduscol, toutes les préconisations faites consistent à enseigner le numérotage et la répartition régulière des numéros sur une ligne graduée. Pourquoi les numéros devraient-ils être régulièrement espacés ? C’est affirmé de manière dogmatique. Ainsi, ce serait en faisant un usage répété d’une graduation régulière que l’enfant apprendrait que lui aussi doit espacer régulièrement les points numérotés. Ce n’est pas en s’appropriant la propriété conceptuelle « +1 répété », celle qui explique cet espacement régulier, que les élèves progresseraient. Il ne conviendrait pas non plus de faire comprendre aux élèves la façon dont l’itération de l’unité est représentée sur une ligne graduée : inclusion des différentes quantités entre elles et ponctualisation de leur désignation. Dans les recommandations du site Eduscol, le pédagogue devrait viser à ce que l’élève produise la bonne réponse sans comprendre. Le bas niveau de ces recommandations pédagogiques est totalement déprimant.

Cette analyse n’est qu’un exemple : depuis le changement de ministère, dès que le site Eduscol promeut telle ou telle pratique pédagogique (déplacement sur une file numérotée notamment), il faudrait analyser précisément ce qui est promu pour montrer que les rédacteurs du document n’ont rien compris au changement de cap qui s’est produit avec les programmes 2015 et qu’ils sont en train de faire s’envoler l’espoir de redressement des performances en calcul que ces programmes avaient fait naitre.

Rémi Brissiaud

Maitre de Conférences honoraire de psychologie cognitive

Membre du conseil scientifique de l'AGEEM

Bibliographie

Brandicourt R (1962). Des principes à la pratique pédagogique. In J. Bandet (Ed) : Les débuts du calcul, 87-108. Paris : Éditions Bourrelier

Brissiaud, R. (octobre 2014) Pourquoi l’école a-t-elle enseigné le comptage-numérotage pendant près de 30 années ? Une ressource à restaurer : un usage commun des mots grandeur, quantité, nombre, numéro, cardinal, ordinal, etc. Texte mis en ligne par la Commission Française pour l’Enseignement des Mathématiques (cfem).

Butterworth, B. (26 février 213) Espace, temps et nombre chez les personnes atteintes de dyscalculie. Intervention au colloque : « Interactions entre espace, temps et nombre : 20 ans de recherches » organisé par Stanislas Dehaene au collège de France

Canac, H. (1955) L'initiation au calcul entre 5 et 7 ans. In F. Brachet, H. Canac & E. Delaunay (ed.), L'enfant et le nombre, p.9-27. Paris : Didier.

Coubart A, Izard V, Spelke ES, Marie J, Streri A. (2014). Dissociation between small and large numerosities in newborn infants. Developmental Science, 17, 11-22

Dehaene, S. (2010) La bosse des maths, 15 ans après. Paris : Odile Jacob.

Dehaene, S. (2012) L’intuition en mathématiques et les démarches algorithmiques. Intervention à la conférence nationale sur l’enseignement des mathématiques. 

Izard, V., Pica, P., Spelke, E. S., & Dehaene, S. (2008). Exact equality and successor function: Two key concepts on the path towards understanding exact numbers. Philosophical psychology, 21(4), 491-505.

Lyons, I. M., Bugden, S., Zheng, S., De Jesus, S., & Ansari, D. (2018). Symbolic number skills predict growth in nonsymbolic number skills in kindergarteners. Developmental Psychology, 54(3), 440-457.

Rocher T. (2008) Lire, écrire, compter : les performances des élèves de CM2 à vingt ans d'intervalle 1987-2007. Note 08.38 de la DEPP ; décembre 2008.

Spelke E. (2017) Core Knowledge, Language, and Number. Language Learning and Development, 13- Issue 2: The Representation of Number: Origins and Development

Vergnaud G. (1987) Les fonctions de l’action et de la symbolisation dans la formation des connaissances chez l’enfant. In Jean Piaget, Pierre Mounoud & Jean-Paul Bronckart (Eds) Encyclopédie de la Pléiade, Volume Psychologie.